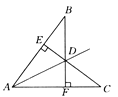
【题目】如图,BF⊥AC于点F,CE⊥AB于点E,BF与CE交于D,且BD=CD.
(1)求证:D在∠BAC的平分线上;
(2)若将条件:BD=CD和结论:D在∠BAC的平分线上互换,结论成立吗?试说明理由.
参考答案:
【答案】(1)证明见解析;(2)成立,理由见解析.
【解析】
(1)先通过“角角边”证明Rt△BED≌Rt△CFD,得到DE=DF,再根据角平分线的性质得出证明;
(2)根据角平分线的性质得到DE=DF,再通过“角边角”证明Rt△BED≌Rt△CFD,得到BD=CD.
(1)证明:∵BF⊥AC,CE⊥AB,
∴∠BED=∠CFD=90°,
在Rt△BED和Rt△CFD中,
∵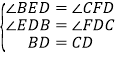 (对顶角相等),
(对顶角相等),
∴Rt△BED≌Rt△CFD(AAS),
∴DE=DF(全等三角形的对应边相等),
∴D在∠BAC的平分线上(到角的两边距离相等的点在角的平分线上);
(2)解:成立.理由如下:
∵点D在∠BAC的平分线上,且BF⊥AC,CE⊥AB,
∴DE=DF,∠BED=∠CFD=90°,
在Rt△BED和Rt△CFD中,
∵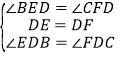 ,
,
∴Rt△BED≌Rt△CFD(ASA),
∴BD=DC(全等三角形的对应边相等).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2016CCTV英语风采大赛中,娄底市参赛选手表现突出,成绩均不低于60分.为了更好地了解娄底赛区的成绩分布情况,随机抽取利了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行了整理,得到如图的两幅不完整的统计图表:
根据所给信息,解答下列问题: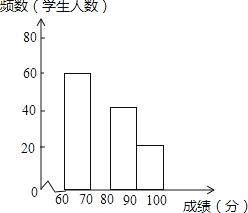
(1)在表中的频数分布表中,m= , n= .成绩
频数
频率
60≤x<70
60
0.30
70≤x<80
m
0.40
80≤x<90
40
n
90≤x≤100
20
0.10
(2)请补全图中的频数分布直方图.
(3)按规定,成绩在80分以上(包括80分)的选手进入决赛.若娄底市共有4000人参数,请估计约有多少人进入决赛? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,下面三个结沦:①AS=AR:②QP∥AR;③△BRP≌△CSP.其中正确的是( )
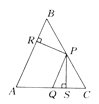
A. ①③ B. ②③ C. ①② D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米,
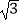 ≈1.732)
≈1.732)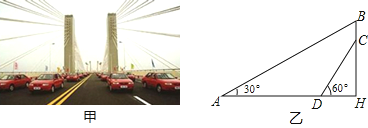
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,能否在AB上确定一点E,使△BDE的周长等于AB的长?请说明理由.
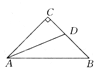
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某水站记录的潮汛期某河一周内的水位变化情况(正号表示水位比前一天上升,负号表示水位比前一天下降,上周的水位恰好达到警戒水位,单位:米)
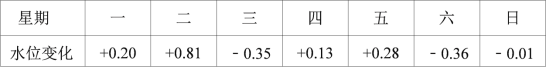
(1)本周哪一天河流的水位最高,哪一天河流的水位最低,它们位于警戒水位之上还是之下,与警戒水位的距离分别是多少?
(2)与上周末相比,本周末河流的水位是上升还是下降了?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如下(规定向南为正,向北为负,单位:km):

①接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
②若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
③若该出租车的计价标准为:行驶路程不超过3km收费10元,超过3km的部分按每千米加1.8元收费,在这过程中该驾驶员共收到车费多少元?
相关试题

