【题目】某商店准备购进甲、乙两种商品.已知甲商品每件进价15元,售价20元;乙商品每件进价35元,售价45元.
(1)若该商店同时购进甲、乙两种商品共100件,恰好用去3100元,求购进甲、乙两种商品各多少件?
(2)若该商店准备购进甲、乙两种商品共100件,其中甲种商品应多于30件且这两种商品全部售出后获利不少于840元,问应该怎样进货,才能使总利润最大,最大利润是多少?(利润=售价﹣进价)
参考答案:
【答案】(1)商店购进甲种商品20件,购进乙种商品80件;(2)应购进甲种商品31件,乙种商品69件,才能使总利润最大,最大利润为895元.
【解析】
试题分析:(1)设购进甲、乙两种商品分别为x件与y件,根据甲种商品件数+乙种商品件数=100,甲商品的总进价+乙种商品的总进价=3100,列出关于x与y的方程组,求出方程组的解即可得到x与y的值,得到购进甲、乙两种商品的件数;
(2)设商店购进甲种商品a件,则购进乙种商品(100﹣a)件,可列出不等式组,求出不等式组的解集,得到a的取值范围,根据a为正整数得出a的值,再表示总利润W,发现W与a成一次函数关系式,且为减函数,故a取最小值时,W最大,即可求出所求的进货方案与最大利润.
解:(1)设购进甲种商品x件,购进乙商品y件,
根据题意得:![]() ,
,
解得:![]() ,
,
答:商店购进甲种商品20件,购进乙种商品80件;
(2)设商店购进甲种商品a件,则购进乙种商品(100﹣a)件,
根据题意列得:![]() ,
,
解得:30<a≤32,
∵总利润W=5a+10(100﹣a)=﹣5a+1000,W是关于a的一次函数,W随a的增大而减小,
∴当a=31时,W有最大值,此时W=895,且100﹣31=69,
答:应购进甲种商品31件,乙种商品69件,才能使总利润最大,最大利润为895元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A.“伊利”纯牛奶消费者服务热线是4008169999,该十个数的中位数为7
B.服装店老板最关心的是卖出服装的众数
C.要了解全市初三近4万名学生2015年中考数学成绩情况,适宜采用全面调查
D.条形统计图能够显示每组中的具体数据,易于比较数据之间的差别
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中,正确的是( )
A.2a2+3a2=5a2
B.(a﹣b)2=a2﹣b2
C.a3a2=a6
D.(﹣2a3)2=8a6 -
科目: 来源: 题型:
查看答案和解析>>【题目】若一个直角三角形的三边长分别为a,b,c,且a2=9,b2=16,则c2为( )
A. 25 B. 7 C. 7或25 D. 9或16
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店第一次用600元购进2B铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价是第一次进价的
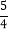 倍,购进数量比第一次少了30支.
倍,购进数量比第一次少了30支.(1)求第一次每支铅笔的进价是多少元?
(2)若要求这两次购进的铅笔按同一价格全部销售完毕后获利不低于420元,问每支售价至少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知等腰直角三角形ABC的直角边长与正方形DEFG的边长均为8 cm,EF与AC在同一条直线上,开始时点A与点F重合,让三角形ABC向左移动,最后点A与点E重合。
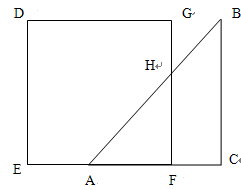
(1)试写出两图形重叠部分的面积 y(cm
 )与线段AF的长度x(cm)之间的函数关系式。
)与线段AF的长度x(cm)之间的函数关系式。 (2)当点A向左移动2cm时,重叠部分的面积是多少?
-
科目: 来源: 题型:
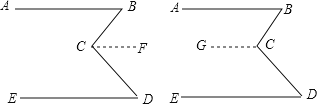
查看答案和解析>>【题目】如图所示,AB∥ED,∠B=46°,∠D=44°,BC垂直于CD吗?下面给出两种添加辅助线的方法,请选择一种,对你作出的结论加以说明.
相关试题

