【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在直线
在直线![]() 上运动(不与点
上运动(不与点![]() 、
、![]() 重合),点
重合),点![]() 在射线
在射线![]() 上运动,且
上运动,且![]() ,设
,设![]() .
.
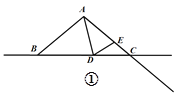
(1)如图①,当点![]() 在边
在边![]() 上时,且
上时,且![]() ,则
,则![]() _______,
_______,![]() _______;
_______;
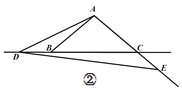
(2)如图②,当点![]() 运动到点
运动到点![]() 的左侧时,其他条件不变,请猜想
的左侧时,其他条件不变,请猜想![]()
和![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
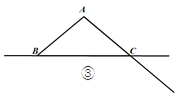
(3)当点![]() 运动到点C的右侧时,其他条件不变,
运动到点C的右侧时,其他条件不变,![]() 和
和![]() 还满足(2)
还满足(2)
中的数量关系吗?请画出图形,并说明理由.
参考答案:
【答案】 64° 32°
【解析】(1)由∠BAC=100°可求出∠ABC=∠ACB=40°,当∠DAC=36°时,根据∠BAD=∠BAC-∠DAC可求出∠BAD的度数,根据∠ADE=∠AED=![]() 可求出∠AED的度数,再根据∠CDE=∠ACB-∠AED求出∠CDE的度数;
可求出∠AED的度数,再根据∠CDE=∠ACB-∠AED求出∠CDE的度数;
(2)由(1)的思路,∠ABC=∠ACB=40°,∠ADE=∠AED=![]() ,∠CDE=∠ACB-∠AED=
,∠CDE=∠ACB-∠AED=![]() ,∠BAD=n-100°,即可得出结论;
,∠BAD=n-100°,即可得出结论;
(3)由(1)的思路,∠ABC=∠ACB=40°,∠ADE=∠AED=![]() ,∠CDE=∠ACB-∠AED=
,∠CDE=∠ACB-∠AED=![]() ,∠BAD=n+100°,即可得出结论;
,∠BAD=n+100°,即可得出结论;
(1)64°,32°
(2)解:![]()
证明:如图②

在![]() 中,
中,![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
∵![]() 是
是![]() 的外角,
的外角,
∴![]() ,
,
∴ ![]() .
.
∵![]()
![]() ,
,
∴![]() ,
,
∴![]() .
.
解:![]() .
.

在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]()
∵![]() 是
是![]() 的外角,
的外角,
∴![]() ,
,
∴ ![]() .
.
∵![]()
![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
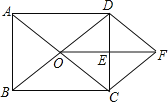
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知直线PQ∥MN,点A在直线PQ上,点C,D在直线MN上,连接AC,AD,∠PAC=50°,∠ADC=30°,AE平分∠PAD,CE平分∠ACD,AE与CE相交于点E.
(1)求∠AEC的度数;
(2)若将图①中的线段AD沿MN向右平移到A1D1如图②所示位置,此时A1E平分∠AA1D1,
CE平分∠ACD1,A1E与CE相交于E,∠PAC=50°,∠A1D1C=30°,求∠A1EC的度数;
(3)若将图①中的线段AD沿MN向左平移到A1D1如图③所示位置,其他条件与(2)相同,求此时∠A1EC的度数(直接写出结果).



-
科目: 来源: 题型:
查看答案和解析>>【题目】某停车场收费标准分为中型汽车和小型汽车两种,某两天这个停车场的收费情况如下表:
中型汽车数量
小型汽车数量
收取费用
第一天
15辆
35辆
360元
第二天
18辆
20辆
300元
(1)中型汽车和小型汽车的停车费每辆多少元?
(2)某天停车场共停车70辆,若收取的停车费用高于500元,则中型汽车至少有多少辆?
-
科目: 来源: 题型:
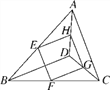
查看答案和解析>>【题目】如图,E,F,G,H分别是边AB,BC,CD,DA的中点,连接EF,FG,GH,HE.
(1)判断四边形EFGH的形状,并证明你的结论;
(2)当BD,AC满足什么条件时,四边形EFGH是正方形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着裕安中学的规模逐渐扩大,学生人数越来越多,学校打算购买校车20辆,现有A和B两种型号校车,如果购买A型号校车6辆,B型号14辆,需要资金580万元;如果购买A型号校车12辆,B型号校车8辆,需要资金760万元.已知每种型号校车的座位数如表所示:
A型号
B型号
座位数(个/辆)
60
30
经预算,学校准备购买设备的资金不高于500万元.(每种型号至少购买1辆)
(1)每辆A型校车和B型校车各多少万元?
(2)请问学校有几种购买方案?且哪种方案的座位数最多,是多少?
-
科目: 来源: 题型:
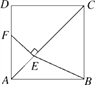
查看答案和解析>>【题目】如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE.
(1)求证:DF=AE;
(2)当AB=2时,求BE2的值.
相关试题

