【题目】如图1,已知点E在正方形ABCD的边BC上,若∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);
(2)如图2,若点E在线段BC上滑动(不与点B,C重合).
①AE=EF是否总成立?请给出证明;
②在图2的AB边上是否存在一点M,使得四边形DMEF是平行四边形?若存在,请给予证明;若不存在,请说明理由.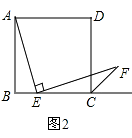
参考答案:
【答案】
(1)
解:如图1,取AB的中点G,连接EG,
△AGE与△ECF全等;
(2)
①若点E在线段BC上滑动时,AE=EF总成立.
证明:如图2,在AB上截取AH=EC,连接EH,
∵AB=BC,
∴BH=BE,
∴△HBE是等腰直角三角形,
∴∠AHE=180°﹣45°=135°,
又∵CF平分正方形的外角,
∴∠ECF=135°,
∴∠AHE=∠ECF.
而∠BAE+∠AEB=∠CEF+∠AEB=90°,
∴∠BAE=∠CEF,
∴△AHE≌△ECF,
∴AE=EF;
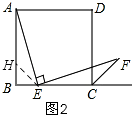
②答:存在,如图3,
过D作DM⊥AE交AB于点M,
则有:DM∥EF,连接ME、DF,
∵在△ADM与△BAE中, 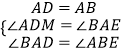 ,
,
∴△ADM≌△BAE(AAS),
∴MD=AE,
∵AE=EF,
∴MD=EF,
∵MD∥EF,
∴四边形DMEP为平行四边形。
【解析】(1)作辅助线,AG=EC,∠BAE=∠CEF,∠AGE=∠ECF=180°﹣45°=135°,则△AGE≌△ECF;(2)①成立,作辅助线,仍然证明△AHE≌△ECF得出结论;②存在,如图3,过D作DM⊥AE交AB于点M,构成四边形DMEF,证明四边形为平行四边形即可.
【考点精析】本题主要考查了平行四边形的性质和平行四边形的判定的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为减少环境污染,自2008年6月1日起,全国的商品零售场所开始实行“塑料购物袋有偿使用制度”(以下简称“限塑令”).某班同学于6月上旬的一天,在某超市门口采用问卷调查的方式,随机调查了“限塑令”实施前后,顾客在该超市用购物袋的情况,以下是根据100位顾客的100份有效答卷画出的统计图表的一部分:
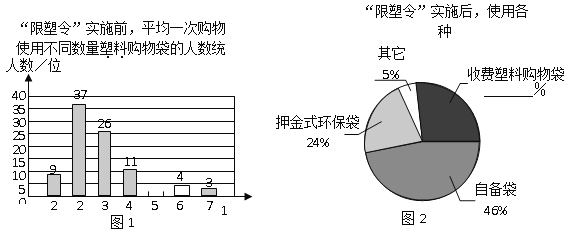
“限塑令”实施后,塑料购物袋使用后的处理方式统计表
处理方式
直接丢弃
直接做垃圾袋
再次购物使用
其它
选该项的人数占
总人数的百分比
5%
35%
49%
11%
请你根据以上信息解答下列问题:
(1)补全图1,“限塑令”实施前,如果每天约有2 000人次到该超市购物.根据这100位顾客平均一次购物使用塑料购物袋的平均数,估计这个超市每天需要为顾客提供多少个塑料购物袋?
(2)补全图2,并根据统计图和统计表说明,购物时怎样选用购物袋,塑料购物袋使用后怎样处理,能对环境保护带来积极的影响.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2=4x的解是( )
A. x=0B. x1=4,x2=0C. x=4D. x=2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个角的两边与另一个角的两边分别平行,结合下图,试探索这两个角之间的关系,并说明你的结论.
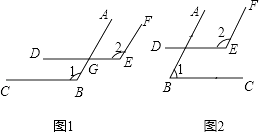
(1)如图1,AB∥EF,BC∥DE.∠1与∠2的关系是: , 理由:;
(2)如图2,AB∥EF,BC∥DE.∠1与∠2的关系是: , 理由: .
(3)由(1)(2)你得出的结论是:如果 , 那么 .
(4)若两个角的两边互相平行,且一个角比另一个角的2倍少30°,则这两个角度数的分别是 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A7B7A8的边长为( )
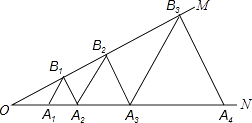
A.6
B.12
C.32
D.64 -
科目: 来源: 题型:
查看答案和解析>>【题目】“在山区建设公路时,时常要打通一条隧道,就能缩短路程”,其中蕴含的数学道理是( )
A. 两点确定一条直线 B. 直线比曲线短
C. 两点之间,线段最短 D. 垂线段最短
-
科目: 来源: 题型:
查看答案和解析>>【题目】地球离太阳约有15000000千米,15000000这个数用科学记数法可以表示为_____.
相关试题

