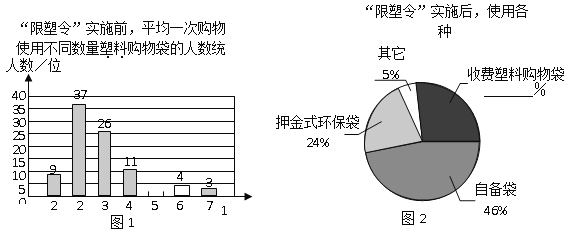
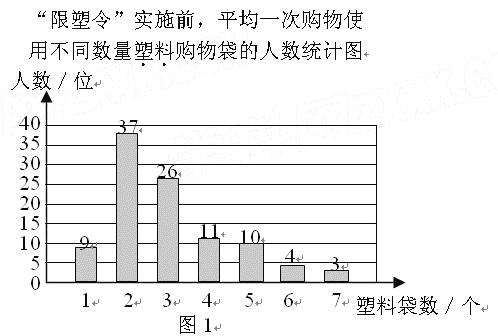
【题目】为减少环境污染,自2008年6月1日起,全国的商品零售场所开始实行“塑料购物袋有偿使用制度”(以下简称“限塑令”).某班同学于6月上旬的一天,在某超市门口采用问卷调查的方式,随机调查了“限塑令”实施前后,顾客在该超市用购物袋的情况,以下是根据100位顾客的100份有效答卷画出的统计图表的一部分:
“限塑令”实施后,塑料购物袋使用后的处理方式统计表
处理方式 | 直接丢弃 | 直接做垃圾袋 | 再次购物使用 | 其它 |
选该项的人数占 总人数的百分比 | 5% | 35% | 49% | 11% |
请你根据以上信息解答下列问题:
(1)补全图1,“限塑令”实施前,如果每天约有2 000人次到该超市购物.根据这100位顾客平均一次购物使用塑料购物袋的平均数,估计这个超市每天需要为顾客提供多少个塑料购物袋?
(2)补全图2,并根据统计图和统计表说明,购物时怎样选用购物袋,塑料购物袋使用后怎样处理,能对环境保护带来积极的影响.
参考答案:
【答案】(1)补全图1见下图.
![]() (个).………………1分
(个).………………1分
(图) ………………1分
这100位顾客平均一次购物使用塑料购物袋的平均数为3个.
![]() .
.
估计这个超市每天需要为顾客提供6000个塑料购物袋.………………2分
(2)图2中,使用收费塑料购物袋的人数所占百分比为![]() .………………2分
.………………2分
根据图表回答正确给1分,例如:由图2和统计表可知,购物时应尽量使用自备袋和押金式环保袋,少用塑料购物袋;塑料购物袋应尽量循环使用,以便减少塑料购物袋的使用量,为环保做贡献. ………………2分
【解析】略
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE.
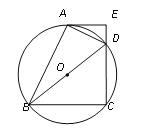
(1)求证:AE⊥CD;
(2)已知AE=4cm,CD=6cm,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县12月份某一天的天气预报为气温﹣2~5℃,该天的温差为( )
A.﹣3℃
B.﹣7℃
C.3℃
D.7℃ -
科目: 来源: 题型:
查看答案和解析>>【题目】将点P(﹣3,4)先向右平移4个单位长度,再向下平移3个单位长度后的坐标是( )
A. (1,7)B. (﹣7,7)C. (1,1)D. (﹣7,1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2=4x的解是( )
A. x=0B. x1=4,x2=0C. x=4D. x=2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个角的两边与另一个角的两边分别平行,结合下图,试探索这两个角之间的关系,并说明你的结论.
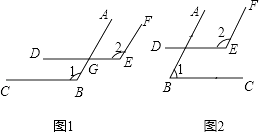
(1)如图1,AB∥EF,BC∥DE.∠1与∠2的关系是: , 理由:;
(2)如图2,AB∥EF,BC∥DE.∠1与∠2的关系是: , 理由: .
(3)由(1)(2)你得出的结论是:如果 , 那么 .
(4)若两个角的两边互相平行,且一个角比另一个角的2倍少30°,则这两个角度数的分别是 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点E在正方形ABCD的边BC上,若∠AEF=90°,且EF交正方形外角的平分线CF于点F.

(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);
(2)如图2,若点E在线段BC上滑动(不与点B,C重合).
①AE=EF是否总成立?请给出证明;
②在图2的AB边上是否存在一点M,使得四边形DMEF是平行四边形?若存在,请给予证明;若不存在,请说明理由.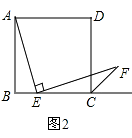
相关试题

