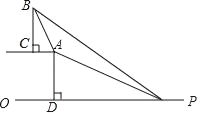
【题目】已知,如图,在坡顶A处的同一水平面上有一座大型纪念碑BC,某同学在斜坡底P处测得该碑的碑顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米到达坡顶A,在坡顶A处又测得该碑的碑顶B的仰角为76°,求纪念碑BC的高度(结果精确到0.1米).(过点A作AD⊥PO,垂足为点D.坡度=AD:PD)(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
参考答案:
【答案】古塔BC的高度约为18.7米.
【解析】
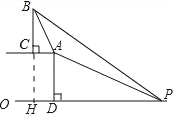
延长BC交OP于H.在Rt△APD中解直角三角形求出AD=10.PD=24.由题意BH=PH.设BC=x.则x+10=24+DH.推出AC=DH=x﹣14.在Rt△ABC中.根据tan76°=![]() ,构建方程求出x即可.
,构建方程求出x即可.
延长BC交OP于H.
∵斜坡AP的坡度为1:2.4,
∴![]() ,
,
设AD=5k,则PD=12k,由勾股定理,得AP=13k,
∴13k=26,
解得k=2,
∴AD=10,
∵BC⊥AC,AC∥PO,
∴BH⊥PO,
∴四边形ADHC是矩形,CH=AD=10,AC=DH,
∵∠BPD=45°,
∴PH=BH,
设BC=x,则x+10=24+DH,
∴AC=DH=x﹣14,
在Rt△ABC中,tan76°=![]() ,即
,即![]() ≈4.01.
≈4.01.
解得:x≈18.7,
经检验x≈18.7是原方程的解.
答:古塔BC的高度约为18.7米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.
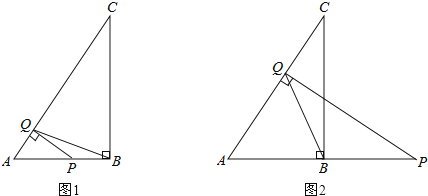
(1)当点P在线段AB上时,求证:△APQ∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.

-
科目: 来源: 题型:
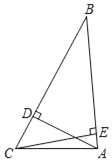
查看答案和解析>>【题目】在锐角△ABC中,AD与CE分别是边BC与AB的高,AB=12,BC=16,S△ABC=48,
求:(1)角B的度数;
(2)tanC的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛一枚均匀硬币正面朝上的概率为
 ,下列说法错误的是
,下列说法错误的是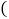
A. 连续抛一枚均匀硬币2次必有1次正面朝上
B. 连续抛一枚均匀硬币10次都可能正面朝上
C. 大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次
D. 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
-
科目: 来源: 题型:
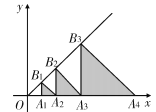
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1,B2,B3…都在直线y=x上,OA1=1,且△B1A1A2,△B2A2A3,△B3A3A4,…△Bn A n A n+1…分别是以A1,A2,A3,…An…为直角顶点的等腰直角三角形,则△B10A10A11的面积是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 抛物线
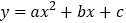 与
与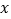 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与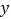 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①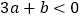 ;②
;②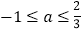 ;③对于任意实数m,
;③对于任意实数m,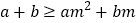 总成立;④关于
总成立;④关于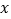 的方程
的方程 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为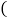
A. 1 个 B. 2 个 C. 3 个 D. 4 个
相关试题

