【题目】图中的网格称之为三角形网格,它的每一个小三角形都是边长为1的正三角形,画出格点△ABC(即△ABC三个顶点都在小正三角形的顶点处),如图所示,请按照下列要求,画出相应的图形,并计算. 
(1)请在①中画出一个与△ABC面积相等,且不全等的格点三角形,并写出相应的面积; 
(2)请在图②和图③中分别画出一个与△ABC相似,且互补全等的格点三角形,并写出相应的相似比k(△ABC与△A′B′C′之比) 

参考答案:
【答案】
(1)解:如图①所示,该三角形的面积为 ![]() ×1×
×1× ![]() =
= ![]() ,
,

(2)解:如图②所示,△ABC∽△A′B′C′,相似比为1:2,

如图③所示,△ABC∽△A′B′C′,相似比为1: ![]() ,
,

【解析】(1)作出一个与原三角形底边公共、高相等的三角形即可;(2)将原三角形的三边分别扩大2倍、 ![]() 倍即可得.
倍即可得.
【考点精析】本题主要考查了等边三角形的性质的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y+6与x-1成正比例,且当x=3时,y=-10.
(1)求y与x的函数关系式;
(2)画出函数的图象.
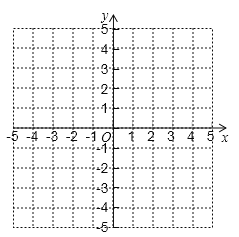
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AOB是一条直线,∠AOC=60°,OD,OE分别是∠AOC和∠BOC的平分线,则图中互补的角有( )
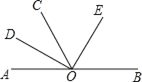
A. 5对 B. 6对 C. 7对 D. 8对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,AE是⊙O的直径,点C是⊙O上的点,连结AC并延长AC至点D,使CD=CA,连结ED交⊙O于点B.
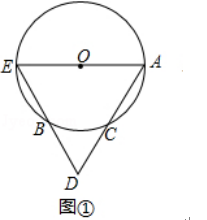
(1)求证:点C是劣弧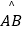 的中点;
的中点;
(2)如图②,连结EC,若AE=2AC=4,求阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】(14分)盘锦红海滩景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用
 (元)及节假日门票费用
(元)及节假日门票费用 (元)与游客x(人)之间的函数关系如图所示.
(元)与游客x(人)之间的函数关系如图所示.
(1)a= ,b= ;
(2)直接写出
 、
、 与x之间的函数关系式;
与x之间的函数关系式;(3)导游小王6月10日(非节假日)带A旅游团,6月20日(端午节)带B旅游团到红海滩景区旅游,两团共计50人,两次共付门票费用3040元,求A、B两个旅游团各多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小芳骑自行车从家出发到野外郊游.从家出发0.5小时到达甲地,游玩一段时间后按原速前往乙地.小芳离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,行驶10分钟时,恰好经过甲地.如图是她们距乙地的路程y(km)与小芳离家x(h)的函数图象.
(1)小芳骑车的速度为 km/h,点H的坐标为 .
(2)小芳从家出发多少小时后被妈妈追上?此时距家的的路程多远?

(3)相遇后,妈妈载上小芳和自行车同时到达乙地(彼此交流时间忽略不计),求小芳比预计时间早几分钟到达乙地?
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),y关于t的函数图象如图所示.
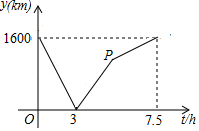
(1)填空:动车甲的速度为(km/h),动车乙的速度为(km/h);
(2)求图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)两车何时相距1200km?
相关试题

