【题目】某中学为了丰富学生的校园体育锻炼生活,决定根据学生的兴趣爱好采购一批体育用品供学生课后锻炼使用,因此学校随机抽取了部分同学就兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题: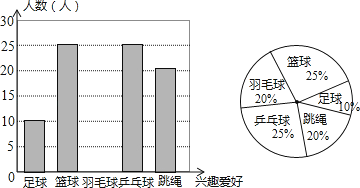
(1)设学校这次调查共抽取了n名学生,直接写出n的值;
(2)请你补全条形统计图;
(3)设该校共有学生1200名,请你估计该校有多少名学生喜欢跳绳?
参考答案:
【答案】
(1)
解:∵喜欢篮球的人数有25人,占总人数的25%,
∴ ![]() =100(人)
=100(人)
(2)
解:∵喜欢羽毛球的人数=100×20%=20人,
∴条形统计图如图
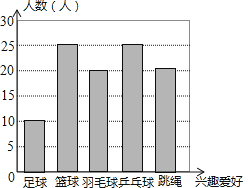
(3)
解:由已知得,1200×20%=240(人).
答;该校约有240人喜欢跳绳
【解析】(1)根据喜欢篮球的人数有25人,占总人数的25%即可得出总人数;(2)根据总人数求出喜欢羽毛球的人数,补全条形统计图即可;(3)求出喜欢跳绳的人数占总人数的20%即可得出结论. 本题考查的是条形统计图,熟知从条形图可以很容易看出数据的大小,便于比较是解答此题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心,大于
 MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC:S△ABC=1:3.其中正确的是__________________.(填所有正确说法的序号)
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC:S△ABC=1:3.其中正确的是__________________.(填所有正确说法的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC与BD交于点O,∠ABC:∠BAD=1:2,BE∥AC,CE∥BD.
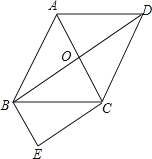
(1)求tan∠DBC的值;
(2)求证:四边形OBEC是矩形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ ABC 是等腰三角形,CA=CB,0°<∠ACB≤90°,点 M 在边 AC 上,点 N在边 BC 上(点 M、点 N 不与所在线段端点重合),BN=AM,连接 AN,BM.射线 AG∥BC,延长 BM 交射线 AG 于点 D,点 E 在直线 AN 上,且 AE=DE.
(1)如图,当∠ACB=90°时,
①求证:△ BCM≌△ACN;
②求∠BDE 的度数;
(2)当∠ACB=ɑ ,其它条件不变时,∠BDE 的度数是 (用含ɑ 的代数式表示).
(3)若△ ABC 是等边三角形,AB=3
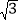 ,点 N 是 BC 边上的三等分点,直线 ED 与直线 BC 交于点 F,请直接写出线段 CF 的长.
,点 N 是 BC 边上的三等分点,直线 ED 与直线 BC 交于点 F,请直接写出线段 CF 的长.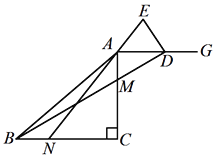
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.
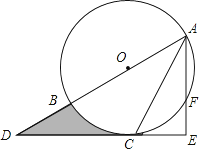
(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
相关试题

