【题目】如图,菱形ABCD的对角线AC与BD交于点O,∠ABC:∠BAD=1:2,BE∥AC,CE∥BD.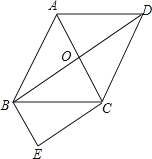
(1)求tan∠DBC的值;
(2)求证:四边形OBEC是矩形.
参考答案:
【答案】
(1)
解:解:∵四边形ABCD是菱形,
∴AD∥BC,∠DBC= ![]() ∠ABC,
∠ABC,
∴∠ABC+∠BAD=180°,
∵∠ABC:∠BAD=1:2,
∴∠ABC=60°,
∴∠BDC= ![]() ∠ABC=30°,
∠ABC=30°,
则tan∠DBC=tan30°= ![]()
(2)
证明:∵四边形ABCD是菱形,
∴AC⊥BD,即∠BOC=90°,
∵BE∥AC,CE∥BD,
∴BE∥OC,CE∥OB,
∴四边形OBEC是平行四边形,
则四边形OBEC是矩形
【解析】(1)由四边形ABCD是菱形,得到对边平行,且BD为角平分线,利用两直线平行得到一对同旁内角互补,根据已知角之比求出相应度数,进而求出∠BDC度数,即可求出tan∠DBC的值;
(2)由四边形ABCD是菱形,得到对角线互相垂直,利用两组对边平行的四边形是平行四边形,再利用有一个角为直角的平行四边形是矩形即可得证.此题考查了矩形的判定,菱形的性质,以及解直角三角形,熟练掌握判定与性质是解本题的关键.
【考点精析】本题主要考查了菱形的性质和矩形的判定方法的相关知识点,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一块四边形田地ABCD,∠D=90°,AB=13m,BC=12m,CD=3m,DA=4m,则该四边形田地ABCD的面积为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C顺时针旋转60°得△ADC,连接OD.当AO=5,BO=4,α=150°时,则CO的长为_________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心,大于
 MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC:S△ABC=1:3.其中正确的是__________________.(填所有正确说法的序号)
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC:S△ABC=1:3.其中正确的是__________________.(填所有正确说法的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了丰富学生的校园体育锻炼生活,决定根据学生的兴趣爱好采购一批体育用品供学生课后锻炼使用,因此学校随机抽取了部分同学就兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
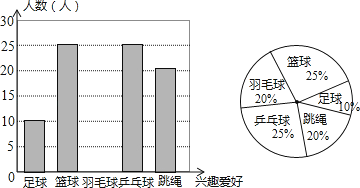
(1)设学校这次调查共抽取了n名学生,直接写出n的值;
(2)请你补全条形统计图;
(3)设该校共有学生1200名,请你估计该校有多少名学生喜欢跳绳? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

相关试题

