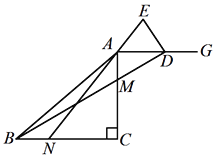
【题目】已知△ ABC 是等腰三角形,CA=CB,0°<∠ACB≤90°,点 M 在边 AC 上,点 N在边 BC 上(点 M、点 N 不与所在线段端点重合),BN=AM,连接 AN,BM.射线 AG∥BC,延长 BM 交射线 AG 于点 D,点 E 在直线 AN 上,且 AE=DE.
(1)如图,当∠ACB=90°时,
①求证:△ BCM≌△ACN;
②求∠BDE 的度数;
(2)当∠ACB=ɑ ,其它条件不变时,∠BDE 的度数是 (用含ɑ 的代数式表示).
(3)若△ ABC 是等边三角形,AB=3![]() ,点 N 是 BC 边上的三等分点,直线 ED 与直线 BC 交于点 F,请直接写出线段 CF 的长.
,点 N 是 BC 边上的三等分点,直线 ED 与直线 BC 交于点 F,请直接写出线段 CF 的长.
参考答案:
【答案】(1)详见解析;90°;(2)α或180-α;(3)![]() 或
或![]() .
.
【解析】
(1)①根据SAS证明即可;
②想办法证明∠ADE+∠ADB=90°即可;
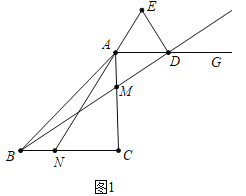
(2)分两种情形讨论求解即可,①如图2中,当点E在AN的延长线上时,②如图3中,当点E在NA的延长线上时;
(3)分两种情形求解即可,①如图4中,当BN=![]() BC=
BC=![]() 时,作AK⊥BC于K.解直角三角形即可.②如图5中,当CN=
时,作AK⊥BC于K.解直角三角形即可.②如图5中,当CN=![]() BC=
BC=![]() 时,作AK⊥BC于K,DH⊥BC于H.
时,作AK⊥BC于K,DH⊥BC于H.
(1)①如图1.
∵CA=CB,BN=AM,∴CB﹣BN=CA﹣AM,即CN=CM.
∵∠ACN=∠BCM,∴△BCM≌△ACN.
②如图1.
∵△BCM≌△ACN,∴∠MBC=∠NAC.
∵EA=ED,∴∠EAD=∠EDA.
∵AG∥BC,∴∠GAC=∠ACB=90°,∠ADB=∠DBC,∴∠ADB=∠NAC,∴∠ADB+∠EDA=∠NAC+∠EAD=∠ADB+∠EDA=180°﹣90°=90°,∴∠BDE=90°.
(2)如图2,当点E在AN的延长线上时.
易证:∠CBM=∠ADB=∠CAN,∠ACB=∠CAD.
∵EA=ED,∴∠EAD=∠EDA,∴∠CAN+∠CAD=∠BDE+∠ADB,∴∠BDE=∠ACB=α.
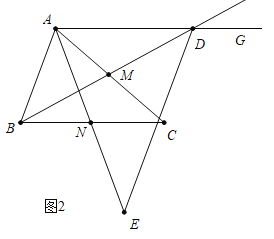
如图3,当点E在NA的延长线上时.
易证:∠1+∠2=∠CAN+∠DAC.
∵∠2=∠ADM=∠CBD=∠CAN,∴∠1=∠CAD=∠ACB=α,∴∠BDE=180°﹣α.
综上所述:∠BDE=α或180°﹣α.
故答案为:α或180°﹣α.
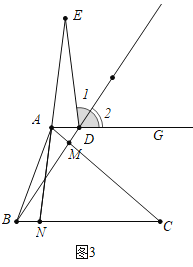
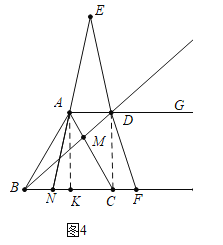
(3)如图4,当BN=![]() BC=
BC=![]() 时,作AK⊥BC于K,连结CD.
时,作AK⊥BC于K,连结CD.
∵AD∥BC,∴![]() =
=![]() =
=![]() ,∴AD=
,∴AD=![]() ,AC=3
,AC=3![]() ,易证△ADC是直角三角形,则四边形ADCK是矩形,△AKN≌△DCF,∴CF=NK=BK﹣BN=
,易证△ADC是直角三角形,则四边形ADCK是矩形,△AKN≌△DCF,∴CF=NK=BK﹣BN=![]() ﹣
﹣![]() =
=![]() .
.
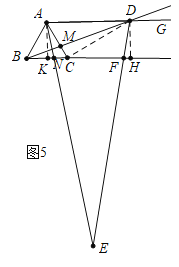
如图5,当CN=![]() BC=
BC=![]() 时,作AK⊥BC于K,DH⊥BC于H.
时,作AK⊥BC于K,DH⊥BC于H.
∵AD∥BC,∴![]() =
=![]() =2,∴AD=6
=2,∴AD=6![]() ,易证△ACD是直角三角形,由△ACK∽△CDH,可得CH=
,易证△ACD是直角三角形,由△ACK∽△CDH,可得CH=![]() AK=
AK=![]() ,由△AKN≌△DHF,可得KN=FH=
,由△AKN≌△DHF,可得KN=FH=![]() ,∴CF=CH﹣FH=4
,∴CF=CH﹣FH=4![]() .
.
综上所述:CF的长为![]() 或4
或4![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了丰富学生的校园体育锻炼生活,决定根据学生的兴趣爱好采购一批体育用品供学生课后锻炼使用,因此学校随机抽取了部分同学就兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
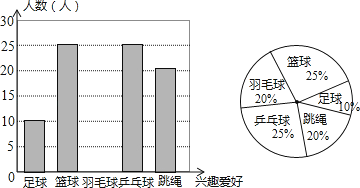
(1)设学校这次调查共抽取了n名学生,直接写出n的值;
(2)请你补全条形统计图;
(3)设该校共有学生1200名,请你估计该校有多少名学生喜欢跳绳? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.
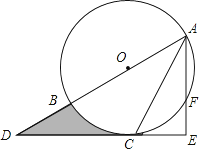
(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图O是边长为9的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于点F,OE∥AC,交BC于点E,则OD+OE+OF的值为( )
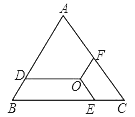
A. 3 B. 6 C. 8 D. 9
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市为庆祝开业举办大酬宾抽奖活动,凡在开业当天进店购物的顾客,都能获得一次抽奖的机会,抽奖规则如下:在一个不透明的盒子里装有分别标有数字1、2、3、4的4个小球,它们的形状、大小、质地完全相同,顾客先从盒子里随机取出一个小球,记下小球上标有的数字,然后把小球放回盒子并搅拌均匀,再从盒子中随机取出一个小球,记下小球上标有的数字,并计算两次记下的数字之和,若两次所得的数字之和为8,则可获得50元代金券一张;若所得的数字之和为6,则可获得30元代金券一张;若所得的数字之和为5,则可获得15元代金券一张;其他情况都不中奖.
(1)请用列表或树状图(树状图也称树形图)的方法(选其中一种即可),把抽奖一次可能出现的结果表示出来;
(2)假如你参加了该超市开业当天的一次抽奖活动,求能中奖的概率P.
相关试题

