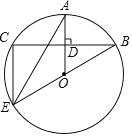
【题目】如图,BE是⊙O的直径,半径OA⊥弦BC,点D为垂足,连AE,EC.
(1)若∠AEC=28°,求∠AOB的度数;
(2)若∠BEA=∠B,BC=6,求⊙O的半径.
参考答案:
【答案】(1)56°;(2)![]() .
.
【解析】
试题分析:(1)根据垂径定理得到![]() =
=![]() ,根据圆周角定理解答;
,根据圆周角定理解答;
(2)根据圆周角定理得到∠C=90°,根据等腰三角形的性质得到∠B=30°,根据余弦的定义求出BE即可.
试题解析:(1)∵OA⊥BC,
∴![]() =
=![]() ,
,
∴∠AEB=∠AEC=28°,
由圆周角定理得,∠AOB=2∠AEB=56°;
(2)∵BE是⊙O的直径,
∴∠C=90°,
∴∠CEB+∠B=90°,
∵∠BEA=∠B,∠AEB=∠AEC,
∴∠B=30°,
∴BE=![]() =
=![]() ,
,
∴⊙O的半径为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育课上,全班男同学进行了100米测验,达标成绩为15秒,下表是某小组8名男生的成绩测试记录,其中“+”表示成绩大于15秒.问:
﹣0.8
+1
﹣1.2
0
﹣0.7
+0.6
﹣0.4
﹣0.1
(1)这个小组男生的达标率为多少?(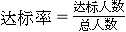 )
)
(2)这个小组男生的平均成绩是多少秒? -
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=﹣x2向右平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上,点A的初始位置表示的数为1,现点A做如下移动:第一次点A向左移动3个单位长度至点A1 , 第2次从点A1向右移动6个单位长度至点A2 , 第3次从点A2向左移动9个单位长度至点A3 , …,按照这种移动方式进行下去,点A4表示的数是 , 如果点An与原点的距离不小于20,那么n的最小值是 .
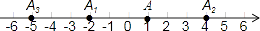
-
科目: 来源: 题型:
查看答案和解析>>【题目】若1﹣(2﹣x)=1﹣x,则代数式2x2﹣7的值是( )
A.﹣5
B.5
C.1
D.﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠A是钝角,∠A与∠B互补,∠B与∠C互余,则∠A与∠C的关系式为( )
A. ∠A -∠C=90° B. ∠A +∠C=90° C. ∠A +∠C=180° D. ∠A =∠C
相关试题

