搜索
【题目】已知关于x的方程 
只有一个实数根，则实数a的取值范围是（ ）
A.a＞0
B.a＜0
C.a≠0
D.a为一切实数
参考答案：
【答案】C
【解析】解：∵方程 
只有一个实数根， ∴函数y= 
和函数y=x2﹣2x+3只有一个交点，
∵函数y=x2﹣2x+3=（x﹣1）2+2，开口向上，对称轴x=1，顶点为（1，2），抛物线交y轴的正半轴，
∴反比例函数y= 应该在一或二象限，
∴a≠0，
故选C．
【考点精析】本题主要考查了反比例函数的图象和二次函数的图象的相关知识点，需要掌握反比例函数的图像属于双曲线．反比例函数的图象既是轴对称图形又是中心对称图形．有两条对称轴：直线y=x和 y=-x．对称中心是：原点；二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，梯形ABCD中，AD∥BC，∠BAD=90°，CE⊥AD于点E，AD=8cm，BC=4cm，AB=5cm．从初始时刻开始，动点P，Q 分别从点A，B同时出发，运动速度均为1cm/s，动点P沿A﹣B﹣﹣C﹣﹣E的方向运动，到点E停止；动点Q沿B﹣﹣C﹣﹣E﹣﹣D的方向运动，到点D停止，设运动时间为xs，△PAQ的面积为ycm2 ， （这里规定：线段是面积为0的三角形）
解答下列问题：
（1）当x=2s时，y=cm2；当x=
s时，y=cm2 ．
（2）当5≤x≤14 时，求y与x之间的函数关系式．
（3）当动点P在线段BC上运动时，求出
S梯形ABCD时x的值．
（4）直接写出在整个运动过程中，使PQ与四边形ABCE的对角线平行的所有x的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题中是真命题的是（ ）
A.经过直线外一点，有且仅有一条直线与一线与已知直线垂直
B.平分弦的直径垂直于弦
C.对角线互相平分且垂直的四边形是菱形
D.反比例函数y=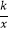
，当k＜0时，y随x的增大而增大 -
科目： 来源： 题型：
查看答案和解析>>【题目】定义：底与腰的比是
的等腰三角形叫做黄金等腰三角形．
如图，已知△ABC中，AC=BC，∠C=36°，BA1平分∠ABC交AC于A1 ．
（1）证明：AB2=AA1AC；
（2）探究：△ABC是否为黄金等腰三角形？请说明理由；（提示：此处不妨设AC=1）
（3）应用：已知AC=a，作A1B1∥AB交BC于B1 ， B1A2平分∠A1B1C交AC于A2 ， 作A2B2∥AB交B2 ， B2A3平分∠A2B2C交AC于A3 ， 作A3B3∥AB交BC于B3 ， …，依此规律操作下去，用含a，n的代数式表示An﹣1An ． （n为大于1的整数，直接回答，不必说明理由） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，
且
于点E，与CD相交于点F，
于点H，交BE于点G.下列结论：①BD=CD；②AD+CF=BD；③
；④AE=CF.其中正确的是____________（填序号）
-
科目： 来源： 题型：
查看答案和解析>>【题目】探索性问题：
已知：b是最小的正整数，且a、b满足（c﹣5）2+|a+b|＝0，请回答问题：
（1）请直接写出a、b、c的值．a＝ ，b＝ ，c＝ ；
（2）数轴上a、b、c三个数所对应的点分别为A、B、C，点A、B、C同时开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动，假设t秒钟过后，若点B与点C之间的距离表示为BC，点A与点B之间的距离表示为AB，点A与点C之间的距离表示为AC．
①t秒钟过后，AC的长度为 （用t的关系式表示）；
②请问：BC﹣AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将矩形ABCD沿BD对折，点A落在E处，BE与CD相交于F，若AD=3，BD=6．
（1）求证：△EDF≌△CBF；
（2）求∠EBC．
相关试题
