Question

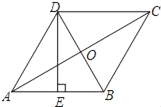
【题目】如图，在菱形ABCD中，AC，BD相交于点O，E为AB的中点，DE⊥AB．

（1）求∠ABC的度数；

（2）如果AC=，求DE的长．

Answer 1

【答案】（1）120°；（2）

【解析】试题分析：（1）根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD，再根据菱形的四条边都相等可得AB=AD，然后求出AB=AD=BD，从而得到△ABD是等边三角形，再根据等边三角形的性质求出△DAB=60°，然后根据两直线平行，同旁内角互补求解即可；

（2）根据菱形的对角线互相平分求出AO，再根据等边三角形的性质可得DE=AO．

解：（1）∵E为AB的中点，DE⊥AB，

∴AD=DB，

∵四边形ABCD是菱形，

∴AB=AD，

∴AD=DB=AB，

∴△ABD为等边三角形．

∴∠DAB=60°．

∵菱形ABCD的边AD∥BC，

∴∠ABC=180°﹣∠DAB=180°﹣60°=120°，

即∠ABC=120°；

（2）∵四边形ABCD是菱形，

∴BD⊥AC于O，AO=AC=×4=2，

由（1）可知DE和AO都是等边△ABD的高，

∴DE=AO=2．