【题目】“校园手机”现象越来越受到社会的关注.“五一”期间,小记者刘铭随机调查了城区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:
(1)求这次调查的家长人数,并补全图①;
(2)求图②中表示家长“赞成”的圆心角的度数;
(3)如果该市有8万名初中生,持“无所谓”态度的学生大约有多少人?
(4)从这次接受调查的家长与学生中随机抽查一个,恰好是“无所谓”态度的概率是多少?

参考答案:
【答案】(1)这次调查的家长人数是400人,补全图见解析;
(2)圆心角的度数是![]()
(3)持“无所谓”态度的学生大约有1.2万名;
(4)恰好是“无所谓”态度的概率是![]()
【解析】分析:(1)利用条形图以及扇形统计图得出总人数即可;(2)利用家长“赞成”所占比例进而得出其圆心角即可;(3)利用持“无所谓”态度的学生所占比例,进而得出答案;(4)利用“无所谓”态度的人数,进而求出其概率.
本题解析:
(1)根据题意可得出: ![]() %=400(人), 家长反对人数:400-40-80=280(人);
%=400(人), 家长反对人数:400-40-80=280(人);
(2)家长“赞成”的圆心角的度数为: ![]() ;
;
(3)市有8万名初中生,持“无所谓”态度的学生大约有: ![]() (4)从这次接受调查的家长与学生中随机抽查一个,恰好是“无所谓”态度的概率是:
(4)从这次接受调查的家长与学生中随机抽查一个,恰好是“无所谓”态度的概率是:
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】完成以下证明,并在括号内填写理由.
已知:如图所示,∠1=∠2,∠A=∠3.
求证:∠ABC+∠4+∠D=180°.
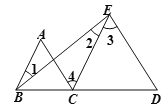
证明:∵∠1=∠2
∴ ∥ ( )
∴∠A=∠4( )
∠ABC+∠BCE=180°( )
即∠ABC+∠ACB+∠4=180°
∵∠A=∠3
∴∠3=
∴ ∥
∴∠ACB=∠D( )
∴∠ABC+∠4+∠D=180°
-
科目: 来源: 题型:
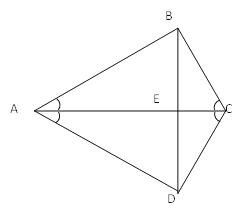
查看答案和解析>>【题目】如图,
(1)如果,AC垂直平分BD.那么,CA平分∠BAD吗?CA平分∠BCD吗?
(2)如果,CA平分∠BAD,且CB⊥AB,CD⊥AD.那么,AC垂直平分BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(-2,1)关于原点对称的点的坐标是()
A. (2,-1) B. (-2,-1) C. (2,1) D. (1,-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正棱锥有六个顶点,所有侧棱长的和为30cm,则每条侧棱的长是______cm.
相关试题

