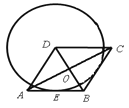
【题目】如图,在菱形ABCD中,AB=2,∠BAD =60,AC交BD于点O,以点D为圆心的⊙D与边AB相切于点E.
(1)、求AC的长;(2)、求证:⊙D与边BC也相切
参考答案:
【答案】(1)、6;(2)、证明过程见解析.
【解析】
试题分析:(1)、根据菱形的性质可得AC=2AO,然后根据AO=AB·cos∠BAO求出AO的长度,然后求出AC的长度;(2)、连接DE,过点D作DF⊥BC,根据菱形四边形以及BD为角平分线得出切线.
试题解析:(1)、∵四边形ABCD是菱形,∠BAD=60 ∴∠BAO=30,∠AOB=90,AC=2AO
∴AO=AB·cos∠BAO=3 ∴AC=6.
(2)、连接DE,过点D作DF⊥BC,垂足为点F∵四边形ABCD是菱形, ∴BD平分∠ABC
∵⊙D与边AB相切于点E,∴DE⊥AB ∵DF⊥BC ∴DF=DE ∴⊙D与边BC也相切.
-
科目: 来源: 题型:
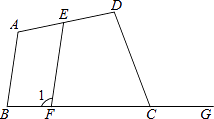
查看答案和解析>>【题目】如图,四边形ABCD中,外角∠DCG=∠A,点E、F分别是边AD、BC上的两点,且EF∥AB.∠D与∠1相等吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂设门市部专卖某产品,该产品每件成本30元,从开业一段时间的每天销售统计中,随机抽取一部分情况如下表所示:
销售单位(元)
50
60
70
75
80
85
…
日销售量(件)
300
240
180
150
120
90
…
假设每天定的售价是不变的,且每天销售情况均服从这种规律.
(1)观察表格判断日销售量与销售价格之间的函数关系,并求出函数关系式;
(2)门市部原设定两名销售员,但当销售量较大时,在每天售出量超过198件时,则必须增派一名营业员才能保证营业有序进行.设营业员每人每天工资为40元,求每件产品应定价多少元,才能使每天门市部纯利润最大?(纯利润=总销售﹣成本﹣营业员工资)
-
科目: 来源: 题型:
查看答案和解析>>【题目】小聪是一名非常爱钻研的七年级学生,他将4块完全一样的三角板(如图1)拼成了一个非常工整的图形(如图2),请教老师以后得知:该图形是一个正方形,并且里面的四边形也是一个正方形.为了作进一步的探究,小明将三角板的三边长用为a,b,c表示(如图3),将两个正方形分别用正方形ABCD和正方形EFGH表示,然后他用两种不同的方法计算了正方形ABCD的面积.
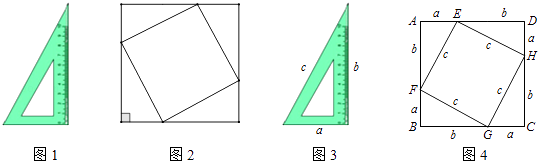
(1)请你用两种不同的方法计算出正方形ABCD面积: 方法一:方法二:
(2)根据(1)中计算结果,你能得到怎么样的结论?
(3)请用文字语言描述(2)中得到的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】(a,﹣6)关于 x 轴对称的点的坐标为( )
A. (﹣a,6) B. (a,6) C. (a,﹣6) D. (﹣a,﹣6)
-
科目: 来源: 题型:
查看答案和解析>>【题目】16的算术平方根和25的平方根的和是( )
A.9
B.-1
C.9或﹣1
D.﹣9或1 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题的是( )
A.如果两个圆心角相等,那么它们所对的弧也相等
B.如果两个圆没有公共点,那么这两个圆外离
C.如果一条直线上有一个点到圆心的距离等于半径,那么这条直线与圆相切
D.如果圆的直径平分弧,那么这条直径就垂直平分这条弧所对的弦
相关试题

