【题目】如图,已知△ABC是⊙O的内接三角形,D是OA延长线上的一点,连接DC,且∠B=∠D=30°,AC=4.
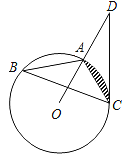
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)求阴影部分的面积.
参考答案:
【答案】(1)CD为⊙O的切线;(2)![]() π﹣4
π﹣4![]() .
.
【解析】
试题分析:(1)连结OC,如图,根据圆周角定理得到∠AOC=2∠B=60°,则利用三角形内角和可计算出∠OCD=90°,所以OC⊥CD,然后根据切线的判定定理可判断CD为⊙O的切线;
(2)先判断△AOC为等边三角形,则OA=AC=4,然后根据扇形面积公式和等边三角形的面积公式,利用S阴影部分=S扇形AOC﹣S△OAC进行计算.
解:(1)直线CD为⊙O的切线.理由如下:
连结OC,如图,
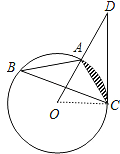
则∠AOC=2∠B=60°,
∵∠D=30°,
∴∠OCD=180°﹣30°﹣60°=90°,
∴OC⊥CD,
∴CD为⊙O的切线;
(2)∵OA=OC,∠AOC=60°,
∴△AOC为等边三角形,
∴OA=AC=4,
∴S阴影部分=S扇形AOC﹣S△OAC
=![]() ﹣
﹣![]() 42
42
=![]() π﹣4
π﹣4![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=﹣
 +bx+c的图象经过A(2,0)、B(0,﹣6)两点.
+bx+c的图象经过A(2,0)、B(0,﹣6)两点.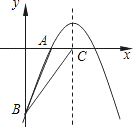
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程xa﹣1﹣3x+2=0是一元二次方程,则a的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和是外角和的3倍,则这个多边形的边数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列图形是将正三角形按一定规律摆放,第一次摆放的图形中有 个正三角形,第二次摆放的图形中有 个正三角形,…以此类推,则第五次摆放的图形中所有的正三角形的个数 .
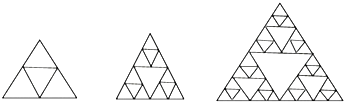
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N(下面是推理过程,请你填空).

解:∵∠BAE+∠AED=180°(已知)
∴ ∥ (同旁内角互补,两直线平行)
∴∠BAE= (两直线平行,内错角相等)
又∵∠1=∠2
∴∠BAE﹣∠1= ﹣
即∠MAE=
∴ ∥ (内错角相等,两直线平行)
∴∠M=∠N(两直线平行,内错角相等)
-
科目: 来源: 题型:
查看答案和解析>>【题目】台球桌的形状是一个长方形,当母球被击打后可能在不同的边上反弹,为了母球最终击中目标球,击球者需作出不同的设计,确定击球的方向,因此,台球既复杂又有趣,台球运动被称为智慧和技能的较量.

问题1:如图(1),如果母球P击中桌边点A,经桌边反弹击中相邻另一条桌边,再次反弹,那么母球P经过的路线BC与PA平行吗?证明你的判断.
问题2:在一张简易球桌ABCD上,如图(2)所示,目标球F、母球E之间有一个G球阻挡,击球者想通过击打母球E先撞球台的CD边,过一次反弹后再撞击F球,他应将E球打到CD边上的哪一点?
请用尺规作图在图(2)中作出这一点.
问题3:如图(3),在简易球台ABCD上,已知AB=4,BC=3.母球P从角落A以45°角击出,在桌子边缘回弹若干次后,最终必将落入 (填A、B、C、D)角落的球袋,在它落入球袋之前,与桌子边缘共回弹了 次;若AB=100,BC=99,母球P还终将会落入某个角落的球袋,则它在落入球袋之前,在桌子边缘总共回弹了 次.
考点:作图—应用与设计作图.
相关试题

