Question

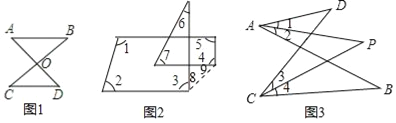
【题目】如图1我们称之为“8字形”，请直接写出∠A，∠B，∠C，∠D之间的数量关系：　 　；

（2）如图2，∠1+∠2+∠3+∠4+∠5+∠6+∠7=　 　度

（3）如图3所示，已知∠1=∠2，∠3=∠4，猜想∠C，∠P，∠D之间的数量关系，并证明．

Answer 1

【答案】（1）∠A+∠D=∠C+∠B；（2）540°；（3）2∠P=∠D+∠B．

【解析】试题分析: （1）根据三角形内角和定理即可得出∠A+∠D=∠C+∠B；

（2）∠6，∠7的和与∠8，∠9的和相等．由多边形的内角和得出答案即可；

（3）先根据“8字形”中的角的规律，可得∠DAP+∠D=∠P+∠DCP①，∠PCB+∠B=∠PAB+∠P②，再根据角平分线的定义，得出∠DAP=∠PAB，∠DCP=∠PCB，将①+②，可得2∠P=∠D+∠B，进而求出∠P的度数；

解：（1）如图1，∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°，∠AOD=∠BOC，

∴∠A+∠D=∠C+∠B；

故答案为：∠A+∠D=∠C+∠B；

（2）∵∠6，∠7的和与∠8，∠9的和相等，

∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠3+∠4+∠5+∠8+∠9=540°．

（3）∠DAP+∠D=∠P+∠DCP，①

∠PCB+∠B=∠PAB+∠P，②

如图3，∵∠DAB和∠BCD的平分线AP和CP相交于点P，

∴∠DAP=∠PAB，∠DCP=∠PCB，

①+②得：

∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠PAB+∠P，

即2∠P=∠D+∠B，

又∵∠D=40度，∠B=36度，

∴2∠P=40°+36°，

∴∠P=38°；

故答案为38°．