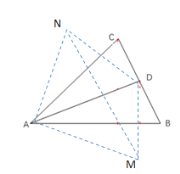
【题目】如图,在面积为3的△ABC中,AB=3,∠BAC=45°,点D是BC边上一点.
(1)若AD是BC边上的中线,求AD的长;
(2)点D关于直线AB和AC的对称点分别为点M、N,求AN的长度的最小值;
(3)若P是△ABC内的一点,求![]() 的最小值.
的最小值.

参考答案:
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)作CE,DF分别垂直于AB于点E,F,已知CE⊥AB,S△ABC=3,∠BAC=45°,可得AE=CE=2,BE=1,因为DF∥CE,AD是BC边上的中线,可得BF=EF=![]() ,在Rt△AFD中利用勾股定理即可求出AD的长.
,在Rt△AFD中利用勾股定理即可求出AD的长.
(2)在Rt△BEC中,求得BC,当AD⊥CB时,AN=AD最小,根据等面积法,即可求出AD.
(3)将△APB绕点A逆时针旋转90°得到△AFE,易知△AFP是等腰直角三角形,∠EAC=135°,作EH⊥BA交BA的延长线于H.在Rt△EAH中,可得![]() EH=AH=2,在Rt△EHC中,求得EC,
EH=AH=2,在Rt△EHC中,求得EC,![]() ,
,![]() 的最小值即为CE的值.
的最小值即为CE的值.
(1)作CE,DF分别垂直于AB于点E,F

∵CE⊥AB,S△ABC=3,∠BAC=45°
∴![]() ,BE=1,
,BE=1,
∵CE,DF分别垂直于AB于点E,F
∴DF∥CE
又∵AD是BC边上的中线
∴![]() ,
,![]()
∴AF=![]()
在Rt△AFD中,![]()
∴![]()
(2)在Rt△BEC中,BC=![]()
当AD⊥CB时,AN=AD最小
根据等面积法,
![]()
得AN=![]()
故答案为:![]()
(3)将△APB绕点A逆时针旋转90°得到△AFE,易知△AFP是等腰直角三角形,∠EAC=135°,作EH⊥BA交BA的延长线于H.

在Rt△EAH中,
∵∠H=90°,∠EAH=45°,![]()
∴EH=AH=2,
在Rt△EHC中,![]()
![]()
∴![]() 的最小值为
的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】浠水县商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
4台
1200元
第二周
5台
6台
1900元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD.
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC;
(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由;
(3)点P是直线BD上一个动点,连接PC、PO ,当点P在直线BD上运动时,请直接写出∠OPC与∠PCD、∠POB的数量关系

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)

⑵-32×2+3×(-2)2
(3)

(4)

(5)已知(x-1)2=4,求x的值.
(6)一个正数的两个平方根分别为a+3和2a+3,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形
 、
、 、
、 、…按如图所示的方式放置.点
、…按如图所示的方式放置.点 、
、 、
、 、…和点
、…和点 、
、 、
、 、…分别在直线
、…分别在直线 和
和 轴上,则点
轴上,则点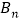 的坐标是__________.(
的坐标是__________.( 为正整数)
为正整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一张长方形纸片ABCD沿EF折叠后,ED与BC交点为G,D、C分别在M、N的位置上,若∠2-∠1=40°,则∠EFC的度数为( )

A. 115°B. 125°C. 135°D. 145°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,点E在边BC上,如果点F是边AD上的点,那么△CDF与△ABE不一定全等的条件是( )
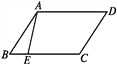
A. DF=BE B. AF=CE
C. CF=AE D. CF∥AE
相关试题

