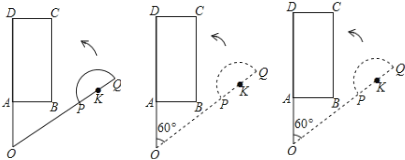
【题目】平面上,矩形ABCD与直径为QP的半圆K如图摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1,让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转,设旋转角为α(0°≤α≤60°).
发现:
(1)当α=0°,即初始位置时,点P 直线AB上(选填“在”或“不在”).
当α= 时,OQ经过点B;
(2)在OQ旋转过程中,α= 时,点P,A间的距离最小?PA最小值为 ;
(3)探究当半圆K与矩形ABCD的边相切时,求sinα的值.
参考答案:
【答案】(1)在,15°;(2)60°,1;(3)![]() 或
或![]() 或
或![]() .
.
【解析】
试题分析:(1)如图1所示,过点P作PA′⊥OD,垂足为A′.在△A′OP中利用利用特殊锐角三角函数可求得OA′=1,由OA=1,从而可求得点A与点A′重合,根据过一点有且只有一条直线与已知直线垂直可知点P在AB上;如图2所示:由△ABO为等腰直角三角形可知∠AOB=45°,从而可求得∠QOQ′=15°;
(2)(2)如图2,连接AP,由OA+AP≥OP,当OP过点A,即α=60°时,等号成立,于是有AP≥OP-OA=2-1=1,当α=60°时,P、A之间的距离最小,即可求得结果;
(3)半圆K与矩形ABCD的边相切,分三种情况;
①如图5,半圆K与BC相切于点T,设直线KT与AD,OQ的初始位置所在的直线分别交于点S,O′,于是得到∠KSO=∠KTB=90°,作KG⊥OO′于G,,在Rt△OSK中,求出OS=![]() =2,在Rt△OSO′中,SO′=OStan60°=2
=2,在Rt△OSO′中,SO′=OStan60°=2![]() ,KO′=2
,KO′=2![]() -
-![]() 3 在Rt△KGO′中,∠O′= =30°,求得KG=
3 在Rt△KGO′中,∠O′= =30°,求得KG=![]() KO′=
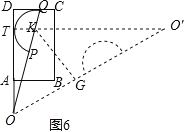
KO′=![]() ,在Rt△KGO中,求得结果;②当半圆K与AD相切于T,如图6,同理可得sinα的值③当半圆K与CD切线时,点Q与点D重合,且为切点,得到α=60°于是结论可求.
,在Rt△KGO中,求得结果;②当半圆K与AD相切于T,如图6,同理可得sinα的值③当半圆K与CD切线时,点Q与点D重合,且为切点,得到α=60°于是结论可求.
试题解析:(1)在,
当OQ过点B时,在Rt△OAB中,AO=AB,
∴∠DOQ=∠ABO=45°,
∴α=60°﹣45°=15°;
(2)如图2,连接AP,
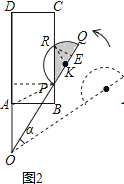
∵OA+AP≥OP,
当OP过点A,即α=60°时,等号成立,
∴AP≥OP﹣OA=2﹣1=1,
∴当α=60°时,P、A之间的距离最小,
∴PA的最小值=1;
(3)半圆K与矩形ABCD的边相切,分三种情况;
①如图5,半圆K与BC相切于点T,设直线KT与AD,OQ的初始位置所在的直线分别交于点S,O′,
则∠KSO=∠KTB=90°,
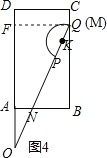
作KG⊥OO′于G,在Rt△OSK中,
OS=![]() =2,
=2,
在Rt△OSO′中,SO′=OStan60°=2![]() ,KO′=2
,KO′=2![]() -
-![]() ,
,
在Rt△KGO′中,∠O′=30°,
∴KG=![]() KO′=
KO′=![]() ,
,
∴在Rt△OGK中,sinα=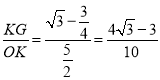 ,
,
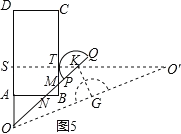
②当半圆K与AD相切于T,如图6,同理可得
sinα=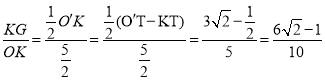 ;
;
③当半圆K与CD切线时,点Q与点D重合,且为切点,=60°,
∴sinα=sin60°=![]() ,
,
综上所述sinα的值为:![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,∠B+∠D=190°,则∠A=_____°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,不一定是轴对称图形的是( )
A.等腰三角形 B.线段 C.钝角 D.直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系内,一个点的坐标为(2,﹣3),则它关于x轴对称的点的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=
 (m≠0)的图象在第一象限交于点C,CD垂直于x轴,垂足为D,若OA=OB=OD=1.
(m≠0)的图象在第一象限交于点C,CD垂直于x轴,垂足为D,若OA=OB=OD=1.(1)求点A、B、D的坐标;
(2)求一次函数与反比例函数的解析式;
(3)在x>0的条件下,根据图象说出反比例函数的值大于一次函数值的x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】学生会准备调查全校七年级学生每天(除课间操外)的课外锻炼时间.
(1)确定调查方式时,甲同学说:“我到1班去调查全体同学”;乙同学说:“我到体育场上去询问参加锻炼的同学”;丙同学说:“我到全校七年级每个班去随机调查一定数量的同学”.你认为调查方式最为合理的是 (填“甲”或“乙”或“丙”);
(2)他们采用了最为合理的调查方法收集数据,并绘制出如图1所示的条形统计图和如图2所示的扇形统计图,请根据图1和图2所提供的信息,将图1中的条形统计图补充完整;(注:图2中相邻两虚线形成的圆心角为30°)

(3)若该校七年级共有1200名同学,请你估计其中每天(除课间操外)课外锻炼时间不大于20分钟的人数,并根据调查情况向学生会提出一条建议.
-
科目: 来源: 题型:
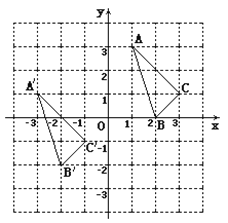
查看答案和解析>>【题目】△ A B C与
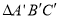 在平面直角坐标系中的位置如图.
在平面直角坐标系中的位置如图.(1)分别写出下列各点的坐标:
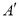 ______ ;
______ ; 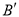 _______ ;
_______ ; 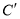 _______ ;
_______ ;(2)说明
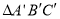 由△ A B C经过怎样的平移得到? ________________________________.
由△ A B C经过怎样的平移得到? ________________________________.(3)若点
 (
(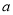 ,
, 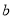 )是△ A B C内部一点,则平移后
)是△ A B C内部一点,则平移后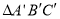 内的对应点
内的对应点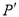 的坐标为 ________ ;
的坐标为 ________ ;(4)求△ A B C的面积..
相关试题

