搜索
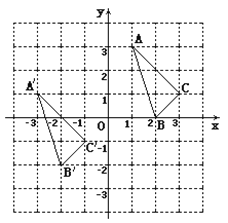
【题目】△ A B C与
在平面直角坐标系中的位置如图.
（1）分别写出下列各点的坐标： 
______ ； 
_______ ； 
_______ ；
（2）说明
由△ A B C经过怎样的平移得到？ ________________________________．
（3）若点
（
， 
）是△ A B C内部一点，则平移后
内的对应点
的坐标为 ________ ；
（4）求△ A B C的面积..
参考答案：
【答案】（1）
（－3,1）; 
（－2，－2）; 
（－1，－1）；(2)先向左平移4个单位，再向下平移2个单位或先向下平移2个单位，再向左平移4个单位;（3）
（a－4，b－2）;（4）2.
【解析】（1）根据网格确定点的坐标；（2）观察两个三角形的一对对应点比如A、A’,再沿着网格左右上下平移即可；（3）平移前后点的坐标的关系：左减右加，上加下减；（4）面积的求法用割补法.
解：（1）
（－3,1）； 
（－2，－2） ； 
（－1，－1） ；
(2)先向左平移4个单位，再向下平移2个单位或先向下平移2个单位，再向左平移4个单位
（3）
（a－4，b－2）
（4）将
补成长方形，减去3个直角三角形的面积得：
6－1.5－0.5－2＝2
“点睛”本题考查了利用平移变换作图，熟练掌握网络结构，根据对应点的坐标确定出找出平移的方法是解题的关键.
-
科目： 来源： 题型：
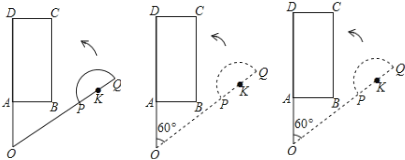
查看答案和解析>>【题目】平面上，矩形ABCD与直径为QP的半圆K如图摆放，分别延长DA和QP交于点O，且∠DOQ＝60°，OQ＝OD＝3，OP＝2，OA＝AB＝1，让线段OD及矩形ABCD位置固定，将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转，设旋转角为α(0°≤α≤60°)．
发现：
（1）当α＝0°，即初始位置时，点P 直线AB上(选填“在”或“不在”)．
当α= 时，OQ经过点B；
（2）在OQ旋转过程中，α= 时，点P，A间的距离最小？PA最小值为 ；
（3）探究当半圆K与矩形ABCD的边相切时，求sinα的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知一次函数y=kx+b（k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数y=
（m≠0）的图象在第一象限交于点C，CD垂直于x轴，垂足为D，若OA=OB=OD=1．（1）求点A、B、D的坐标；
（2）求一次函数与反比例函数的解析式；
（3）在x＞0的条件下，根据图象说出反比例函数的值大于一次函数值的x的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】学生会准备调查全校七年级学生每天(除课间操外)的课外锻炼时间．
（1）确定调查方式时，甲同学说：“我到1班去调查全体同学”；乙同学说：“我到体育场上去询问参加锻炼的同学”；丙同学说：“我到全校七年级每个班去随机调查一定数量的同学”．你认为调查方式最为合理的是 （填“甲”或“乙”或“丙”）；
（2）他们采用了最为合理的调查方法收集数据，并绘制出如图1所示的条形统计图和如图2所示的扇形统计图，请根据图1和图2所提供的信息，将图1中的条形统计图补充完整；(注：图2中相邻两虚线形成的圆心角为30°)
（3）若该校七年级共有1200名同学，请你估计其中每天(除课间操外)课外锻炼时间不大于20分钟的人数，并根据调查情况向学生会提出一条建议．
-
科目： 来源： 题型：
查看答案和解析>>【题目】师生积极为地震灾区捐款，在得知灾区急需帐篷后，立即到当地的一家帐篷厂采购，该厂生产的帐篷有两种规格：可供3人居住的小帐篷，价格每顶160元；可供10人居住的大帐篷，价格每顶400元。学校用去捐款96000元采购，正好可供2300人临时居住。
（1）求该校采购了多少顶3人小帐篷？多少顶10人大帐篷？
（2）学校计划租用甲、乙两种型号的卡车共20辆，将这批帐篷紧急运往灾区，已知甲型卡车每辆可同时装运4顶小帐篷和11顶大帐篷，乙型卡车每辆可同时装运12顶小帐篷和7顶大帐篷。如何安排甲、乙两种卡车，可一次性将这批帐篷运往灾区？有哪几种方案？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果ab>0,a+b<0,那么a,b的符号是( )
A. a>0,b>0 B. a>0, b<0 C. a<0 ,b>0 D. a<0, b<0
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知| a |=3，| b |=5，且ab＜0，求a+b的值．
相关试题
