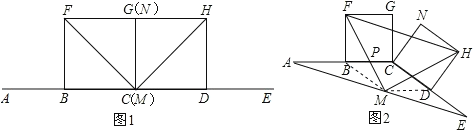
【题目】在图1、图2中,线段AC=CE,点B是线段AC的中点,点D是线段CE的中点,四边形BCGF和CDHN都是正方形,AE的中点是M.如图1,点E在AC的延长线上,点N与点G重合时,点M与点C重合,容易证明FM=MH,FM⊥HM;现将图1的CE绕点C顺时针旋转一个锐角,得到图2,判断△FMH的形状,并证明你的结论.

参考答案:
【答案】△FMH是等腰直角三角形,理由见解析
【解析】分析:连接BM,MD,MF交AC于P,根据三角形中位线定理求出MD∥BC,![]() MB∥CD,
MB∥CD,![]() 得出平行四边形
得出平行四边形![]() ,求出∠CBM=∠CDM,根据SAS证△FBM≌△HDM,推出FM=MH,∠FMB=∠MHD,∠BFM=∠DHM,即可求出
,求出∠CBM=∠CDM,根据SAS证△FBM≌△HDM,推出FM=MH,∠FMB=∠MHD,∠BFM=∠DHM,即可求出![]() 即可得出答案.
即可得出答案.
详解:△FMH是等腰直角三角形,
证明:连接BM,MD,MF交AC于P,
∵B、D.M分别是AC、CE、AE的中点,
∴MD∥BC,![]()
MB∥CD,![]()
∴四边形BCDM是平行四边形,
∴∠CBM=∠CDM,
∵![]()
∴∠FBM=∠MDH,
∵FB=HD,BM=DM,
∴△FBM≌△HDM,
∴FM=MH,∠FMB=∠MHD,∠BFM=∠DHM,
∴![]()
∴△FMH是等腰直角三角形.
-
科目: 来源: 题型:
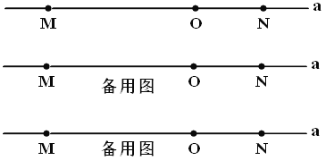
查看答案和解析>>【题目】如图,直线
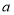 上有
上有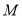 、
、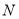 两点,
两点,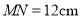 ,点
,点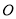 是线段
是线段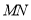 上的一点,
上的一点,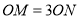 .
.
(1)填空:
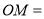 ______
______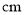 ,
,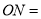 ______
______ ;
;(2)若点
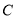 是线段
是线段 上一点,且满足
上一点,且满足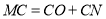 ,求
,求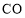 的长;
的长;(3)若动点
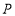 、
、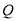 分别从
分别从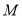 、
、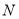 两点同时出发,向右运动,点
两点同时出发,向右运动,点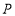 的速度为
的速度为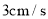 ,点
,点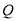 的速度为
的速度为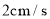 .设运动时间为
.设运动时间为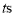 ,当点
,当点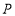 与点
与点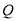 重合时,
重合时,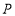 、
、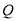 两点停止运动.
两点停止运动.①当
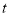 为何值时,
为何值时,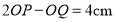 ?
?②当点
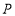 经过点
经过点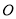 时,动点
时,动点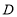 从点
从点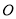 出发,以
出发,以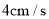 的速度也向右运动,当点
的速度也向右运动,当点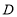 追上点
追上点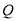 后立即返回,以
后立即返回,以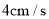 的速度向点
的速度向点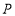 运动,遇到点
运动,遇到点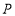 后再立即返回,以
后再立即返回,以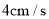 的速度向点
的速度向点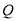 运动,如此往返,直到点
运动,如此往返,直到点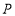 、
、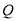 停止运动时,点
停止运动时,点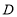 也停止运动.求出在此过程中点
也停止运动.求出在此过程中点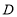 运动的总路程是多少?
运动的总路程是多少? -
科目: 来源: 题型:
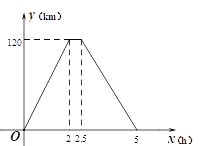
查看答案和解析>>【题目】在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回甲地.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的关系如图所示.
根据图像回答下列问题:
(1)汽车在乙地卸货停留 (h);
(2)求汽车返回甲城时y与x的函数解析式,并写出定义域;
(3)求这辆汽车从甲地出发4 h时与甲地的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有三点A、B、C,请根据图回答下列问题:

(1)若将点B向左平移3个单位后,则A、B、C这三个点所表示的数谁最小?是多少?
(2)若将点A向右平移4个单位后,则A、B、C这三个点所表示的数谁最大?最大的数比最小的数大多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?请列出二元一次方程组解答此问题.
(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置.1.设原来每天安排x名工人生产G型装置,后来补充m名新工人,求x的值(用含m的代数式表示)2.请问至少需要补充多少名新工人才能在规定期内完成总任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小虫从某点O出发在一直线上来回爬行,假定向右爬行的路程记为正,向左爬行的路程记为负,爬过的路程依次为(单位:cm):
+5,﹣3,+10,﹣8,﹣6,+12,﹣10.
问:
(1)请说明小虫最后的具体位置?
(2)小虫离开出发点O最远是多少厘米?
(3)在爬行过程中,如果每爬行1cm奖励三粒芝麻,则小虫共可得到多少粒芝麻?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解方程:3x+5=x+2请按所给导语,填写完整.
解:移项,得3x____=2____,(依据:_____).
合并同类项,得______,
系数化为1,得_____,(依据:______).
(2)解方程:2(x+15)=18﹣3(x﹣9).
相关试题

