【题目】如图,已知A,B两点的坐标分别为(2 ![]() ,0),(0,10),M是△AOB外接圆⊙C上的一点,且∠AOM=30°,则点M的坐标为 .
,0),(0,10),M是△AOB外接圆⊙C上的一点,且∠AOM=30°,则点M的坐标为 . 
参考答案:
【答案】(4 ![]() ,4)
,4)
【解析】解:∵A,B两点的坐标分别为(2 ![]() ,0),(0,10),
,0),(0,10),
∴OB=10,OA=2 ![]() ,
,
∴AB= ![]() =4
=4 ![]() ,
,
∵∠AOB=90°,
∴AB是直径,CM=2 ![]() ,
,
∴Rt△AOB外接圆的圆心为AB中点,
∴C点坐标为( ![]() ,5),
,5),
过点C作CF∥OA,过点M作ME⊥OA于E交CF于F,作CN⊥OE于N,如图所示:
则ON=AN= ![]() OA=
OA= ![]() ,
,
设ME=x,
∵∠AOM=30°,
∴OE= ![]() x
x
∴∠CFM=90°,
∴MF=5﹣x,CF= ![]() x﹣
x﹣ ![]() ,CM=2
,CM=2 ![]() ,
,
在△CMF中,根据勾股定理得:( ![]() x﹣
x﹣ ![]() )2+(5﹣x)2=(2
)2+(5﹣x)2=(2 ![]() )2 ,
)2 ,
解得:x=4或x=0(舍去),
∴OE= ![]() x=4
x=4 ![]()
故答案为:(4 ![]() ,4).
,4).
由勾股定理求出AB的长,由圆周角定理得出AB为直径,求出半径和圆心C的坐标,过点C作CF∥OA,过点P作ME⊥OA于E交CF于F,作CN⊥OE于N,设ME=x,得出OE= ![]() x,在△CMF中,根据勾股定理得出方程,解方程即可.
x,在△CMF中,根据勾股定理得出方程,解方程即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知等腰三角形的一边长等于8cm,一边长等于9cm,求它的周长;
(2)等腰三角形的一边长等于6cm,周长等于28cm,求其他两边的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(﹣
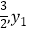 ),(
),(  )是抛物线上两点,则y1<y2其中结论正确的是( )
)是抛物线上两点,则y1<y2其中结论正确的是( ) 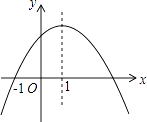
A.①②
B.②③
C.②④
D.①③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AD是∠BAC的平分线,E、F分别为AB、AC上的点,且∠EDF+∠EAF=180°,求证DE=DF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC=2
 ,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则BE的长是 .
,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则BE的长是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠ACD是△ABC的外角,∠A=40°,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.
(1)求∠E的度数.
(2)请猜想∠A与∠E之间的数量关系,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

相关试题

