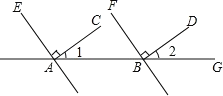
【题目】如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?
因为∠1=35°,∠2=35°(已知),所以∠1=∠2.所以___∥___( ).
又因为AC⊥AE(已知),所以∠EAC=90°( )
所以∠EAB=∠EAC+∠1=125°.
同理可得,∠FBG=∠FBD+∠2=__ °.
所以∠EAB=∠FBG( ).
所以___∥___(同位角相等,两直线平行).
参考答案:
【答案】AC;BD;同位角相等,两直线平行;垂直的定义;125;等量代换;AE;BF.
【解析】
根据同位角相等,两直线平行得到AC∥BD,根据垂直及等量代换得到∠EAB=∠FBG,根据同位角相等,两直线平行证明结论.
因为∠1=35°,∠2=35°(已知),
所以∠1=∠2.
所以AC∥BD(同位角相等,两直线平行).
又因为AC⊥AE(已知),
所以∠EAC=90°.(垂直的定义)
所以∠EAB=∠EAC+∠1=125°.
同理可得,∠FBG=∠FBD+∠2=125°.
所以∠EAB=∠FBG(等量代换).
所以AE∥BF(同位角相等,两直线平行).
故答案为:AC;BD;同位角相等,两直线平行;垂直的定义;125;等量代换;AE;BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班为了从甲、乙两同学中选出班长,进行了一次演讲答辩和民主测评,
 ,
, ,
, ,
, ,
, 五位老师作为评委,对演讲答辩情况进行评价,结果如下表:演讲答辩得分表,另全班
五位老师作为评委,对演讲答辩情况进行评价,结果如下表:演讲答辩得分表,另全班 位同学则参与民主测评进行投票,结果如下图:民主测评统计图
位同学则参与民主测评进行投票,结果如下图:民主测评统计图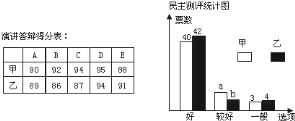
规定:演讲得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评得分
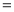 “好”票数
“好”票数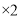 分+“较好”票数
分+“较好”票数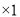 分+“一般”票数
分+“一般”票数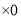 分.
分. 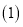 求甲、乙两位选手各自演讲答辩的平均分;
求甲、乙两位选手各自演讲答辩的平均分;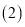 试求民主测评统计图中
试求民主测评统计图中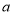 、
、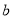 的值是多少?
的值是多少?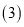 若演讲答辩得分和民主测评得分按
若演讲答辩得分和民主测评得分按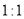 的权重比计算两位选手的综合得分,则应选取哪位选手当班长?
的权重比计算两位选手的综合得分,则应选取哪位选手当班长? -
科目: 来源: 题型:
查看答案和解析>>【题目】为增强公民的节约意识,合理利用天然气资源,某市自
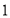 月
月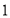 日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:每月用气量
单价(元
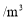 )
)不超出
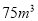 的部分
的部分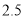
超出
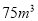 不超过
不超过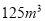 的部分
的部分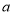
超出
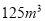 的部分
的部分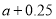
(1)若某用户
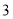 月份用气量为
月份用气量为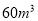 ,交费多少元?
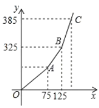
,交费多少元?(2)调价后每月支付燃气费用
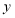 (单位:元)与每月用气量
(单位:元)与每月用气量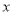 (单位:
(单位: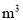 )的关系如图所示,求
)的关系如图所示,求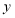 与
与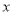 的解析式及
的解析式及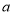 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD的顶点A、D分别落在x轴、y轴,OD=2OA=6,AD:AB=3:1.则点B的坐标是_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】初三(1)班要从2男2女共4名同学中选人做晨会的升旗手.
(1)若从这4人中随机选1人,则所选的同学性别为男生的概率是 .
(2)若从这4人中随机选2人,求这2名同学性别相同的概率.
-
科目: 来源: 题型:
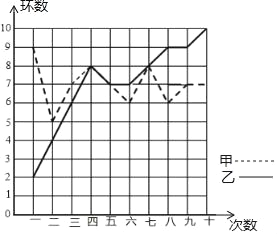
查看答案和解析>>【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:
(1)请将下表补充完整:(参考公式:方差S2=
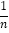 [(x1﹣
[(x1﹣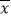 )2+(x2﹣
)2+(x2﹣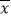 )2+…+(xn﹣
)2+…+(xn﹣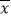 )2])
)2])平均数
方差
中位数
甲
7
7
乙
5.4
(2)请从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一个水池,其底面是边长为16尺的正方形,一根芦苇AB生长在它的正中央,高出水面部分BC的长为2尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′,则这根芦苇AB的长是( )
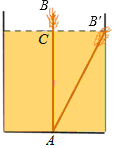
A. 15尺B. 16尺C. 17尺D. 18尺
相关试题

