【题目】如图所示,AB∥CD,试解决下列问题:
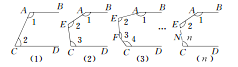
(1)在图(1)中,∠1+∠2等于多少度?请说明理由;
(2)在图(2)中∠1+∠2+∠3等于多少度?请说明理由;
(3)在图(n)中,试探究∠1+∠2+∠3+∠4+…+∠n等于多少度.
参考答案:
【答案】(1) ∠1+∠2=180°, 理由见解析; (2)∠1+∠2+∠3=360°,理由见解析; (3)∠1+∠2+∠3+∠4+…+∠n=180°(n- 1).
【解析】试题分析: (1)根据平行线的性质推出即可;
(2)根据同旁内角互补,两直线平行推出即可;
(3)根据(1)(2)的结果得出即可.
试题解析:
(1)因为AB∥CD,
所以∠1+∠2=180°(两直线平行,同旁内角互补).
(2)如图(1)所示,过点E作EF平行于AB,
因为AB∥CD,AB∥EF,
所以CD∥EF,
所以∠1+∠AEF=180°,∠FEC+∠3=180°,
所以∠1+∠2+∠3=360°.
(3)如图(2)所示,过点E,F分别作EG,FH平行于AB,
因为AB∥CD,
所以AB∥EG∥FH∥CD,
所以∠1+∠AEG=180°,∠GEF+∠EFH=180°,∠HFC+∠4=180°,
所以∠1+∠2+∠3+∠4=540°.
如图(4)所示,根据上述规律,显然作(n- 2)条辅助线,运用(n- 1)次两条直线平行,同旁内角互补,即可得到∠1+∠2+∠3+∠4+…+∠n=180°(n- 1).
-
科目: 来源: 题型:
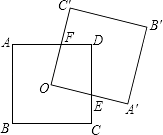
查看答案和解析>>【题目】如图,正方形ABCD的对角线相交于点O,点O是正方形A′B′C′O的一个顶点.如果两个正方形的边长都等于2,那么正方形A′B′C′OA绕O点无论怎样转动,两个正方形重叠的部分的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小丽和小华想利用摸球游戏决定谁去参加市里举办的书法比赛,游戏规则是:在一个不透明的袋子里装有除数字外完全相同的4个小球,上面分别标有数字2,3,4,5.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为偶数,则小丽去参赛;否则小华去参赛.
(1)用列表法或画树状图法,求小丽参赛的概率.
(2)你认为这个游戏公平吗?请说明理由.
-
科目: 来源: 题型:
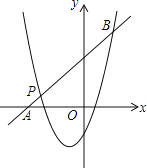
查看答案和解析>>【题目】已知二次函数y1=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.
(1)求m,n的值.
(2)如图,一次函数y2=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA:PB=1:5,求一次函数的表达式.
(3)直接写出y1>y2时x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,用点A(3,1)表示放置3个胡萝卜、1棵青菜,点B(2,3)表示放置2个胡萝卜、3棵青菜.

(1)写出其他各点C,D,E,F所表示的意义;
(2)若一只兔子从A到达B(顺着方格线走),有以下几条路可以选择:①A→C→D→B;②A→F→D→B;③A→F→E→B.则走哪条路吃到的胡萝卜最多?走哪条路吃到的青菜最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中选择一些横、纵坐标满足下面条件的点,标出它们的位置看看它们在第几象限或哪条坐标轴上:
(1)点P(x,y)的坐标满足xy>0;
(2)点P(x,y)的坐标满足xy<0;
(3)点P(x,y)的坐标满足xy=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)x2+5x+7=3x+11
(2)x(2x﹣5)=4x﹣10.
相关试题

