【题目】同学们知道:“在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.”
(1)请写出它的逆命题 ;该逆命题是一个 命题(填“真”或“假”)
(2)若你的判断是真命题请写出证明过程(要求画图,并写出已知,求证).若是假命题,请说明理由.
参考答案:
【答案】(1)在直角三角形中,如果一个锐角等于30度,那么它所对的直角边等于斜边的一半,真;(2)已知,在Rt△ABC中,∠A=30°,∠ACB=90°.求证:BC=![]() AB.
AB.
【解析】
(1)写出逆命题,并判断是真命题;
(2)首先写出已知、求证,画出图形,借助等边三角形的判定和性质证明或借助三角形的外接圆证明.
解:(1)原命题的逆命题为:在直角三角形中,如果一个锐角等于30度,那么它所对的直角边等于斜边的一半,该逆命题是一个真命题;
(2)已知,在Rt△ABC中,∠A=30°,∠ACB=90°.
求证:BC=![]() AB.
AB.
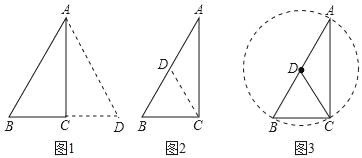
证明:
证法一:如图1所示,延长BC到D,使CD=BC,连接AD,易证AD=AB,∠BAD=60°.
∴△ABD为等边三角形,
∴AB=BD,
∴BC=CD=![]() AB,即BC=
AB,即BC=![]() AB.
AB.
证法二:如图2所示,取AB的中点D,
连接DC,有CD=![]() AB=AD=DB,
AB=AD=DB,
∴∠DCA=∠A=30°,∠BDC=∠DCA+∠A=60°.
∴△DBC为等边三角形,
∴BC=DB=![]() AB,即BC=
AB,即BC=![]() AB.
AB.
证法三:如图3所示,在AB上取一点D,使BD=BC,
∵∠B=60°,
∴△BDC为等边三角形,
∴∠DCB=60°,∠ACD=90°﹣∠DCB=90°﹣60°=30°=∠A.
∴DC=DA,即有BC=BD=DA=![]() AB,
AB,
∴BC=![]() AB.
AB.
证法四:如图3所示,作△ABC的外接圆⊙D,∠C=90°,AB为⊙O的直径,
连DC,有DB=DC,∠BDC=2∠A=2×30°=60°,
∴△DBC为等边三角形,
∴BC=DB=DA=![]() AB,即BC=
AB,即BC=![]() AB.
AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司共有A,B,C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图
各部门人数及每人所创年利润统计表部门
员工人数
每人所创的年利润/万元
A
5
10
B
b
8
C
c
5

(1)①在扇形图中,C部门所对应的圆心角的度数为
②在统计表中,b= , c=
(2)求这个公司平均每人所创年利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】[知识生成]通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.例如:如图①是一个长为
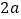 ,宽为
,宽为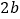 的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题:
的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题: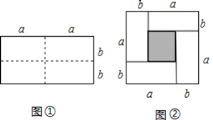
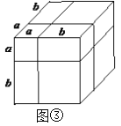
(1)图②中阴影部分的正方形的边长是________________;
(2)请用两种不同的方法求图②中阴影部分的面积:
方法1:________________________;方法2:_______________________;
(3)观察图②,请你写出
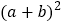 、
、 、
、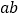 之间的等量关系是__________;
之间的等量关系是__________;(4)根据(3)中的等量关系解决如下问题:若
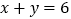 ,
,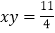 ,则
,则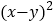 =________;
=________;[知识迁移]
类似地,用两种不同的方法计算同一几何体的体积,也可以得到一个恒等式.
(5)根据图③,写出一个代数恒等式:____________________________;
(6)已知
 ,
,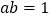 ,利用上面的规律求
,利用上面的规律求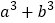 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A篮球、B乒乓球、C跳绳、D踢毽子,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:

(1)这次被调查的学生共有人;
(2)请你将条形统计图补充完成;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答). -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司欲招聘一名部门经理,对甲、乙、丙三名候选人进行了三项素质测试.各项测试成绩如表格所示:
测试项目
测试成绩
甲
乙
丙
专业知识
74
87
90
语言能力
58
74
70
综合素质
87
43
50
(1)如果根据三次测试的平均成绩确定人选,那么谁将被录用?
(2)根据实际需要,公司将专业知识、语言能力和综合素质三项测试得分按4:3:1的比例确定每个人的测试总成绩,此时谁将被录用?
(3)请重新设计专业知识、语言能力和综合素质三项测试得分的比例来确定每个人的测试总成绩,使得乙被录用,若重新设计的比例为x:y:1,且x+y+1=10,则x= ,y= .(写出x与y的一组整数值即可).
-
科目: 来源: 题型:
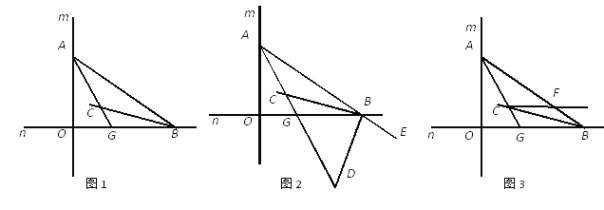
查看答案和解析>>【题目】如图1,直线m与直线n垂直相交于O,点A在直线m上运动,点B 在直线n上运动,AC、BC分别是∠BAO和∠ABO的角平分线.
(1)求∠ACB的大小;
(2)如图2,若BD是△AOB的外角∠OBE的角平分线,BD与AC相交于点D,点A、B在运动的过程中,∠ADB的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值;
(3)如图3,过C作直线与AB交于F,且满足∠AGO-∠BCF=45°,求证:CF∥OB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组

请结合题意,完成本题解答过程.
(1)解不等式①,得 ,依据是 .
(2)解不等式②,得 .
(3)解不等式③,得 .
(4)把不等式①,②和③的解集在数轴上表示出来.
(5)从图中可以找出三个不等式解集的公共部分,得不等式组的解集 .
(6)根据不等式组的解集确立出该不等式组的最大整数解为 .
相关试题

