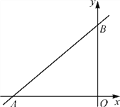
【题目】如图,直线y=kx+6与x轴,y轴分别相交于点A,B,O为坐标原点,点A的坐标为(-8,0).
(1)求k的值;
(2)若点P(x,y)是第二象限内直线上的一个动点,在点P的运动过程中,试写出△OPA的面积S与x之间的函数关系式,并写出自变量的取值范围;
(3)若点P(0,m)为射线BO(B,O两点除外)上的一动点,过点P作PC⊥y轴交直线AB于C,连接PA.设△PAC的面积为S′,求S′与m的函数关系式,并写出自变量m的取值范围.
参考答案:
【答案】(1)![]() (2)S=3x+24(-8<x<0)(3) S′=
(2)S=3x+24(-8<x<0)(3) S′=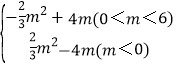
【解析】(1)将点A的坐标代入直线y=kx+6中,即可求得k的值.
(2)点P的纵坐标就是三角形OPA的高,直接写出面积公式.
(3)P,C两点的纵坐标相等,求出C点的横坐标,用m表示PC,再用面积公式.分0<m<6和m<0讨论.
解:(1)将A(-8,0)代入直线y=kx+6,得k=![]() .
.
(2)由题意,得S=![]() OA·y=
OA·y=![]() ×8(
×8(![]() x+6)=3x+24(-8<x<0).
x+6)=3x+24(-8<x<0).
(3)∵PC⊥y轴,P(0,m),∴C点的纵坐标为m.
则![]() x+6=m,
x+6=m,
∴x=![]() .∴C(
.∴C(![]() ,m).∴PC=
,m).∴PC=![]() .
.
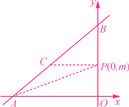
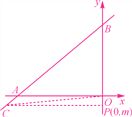
图1 图2
分两种情况:①如图1,当0<m<6时,
S′=![]() OP·PC=
OP·PC=![]() m·
m·![]() =-
=-![]() m2+4m.
m2+4m.
②如图2,当m<0时,
S′=![]() OP·PC=
OP·PC=![]() (-m)·
(-m)·![]() =
=![]() m2-4m.
m2-4m.
综上S′=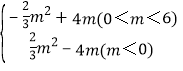 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|a-1|+|b+2|+|3c-6|=0,比较a,b,c的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式运算正确的是( )
A.3x+3y=6xy
B.7x﹣5x=2x2
C.16y2﹣7y2=9
D.19a2b﹣9ba2=10a2b -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,二次函数
 的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=
的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO= .
.
(1)求这个二次函数的表达式;
(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由;
(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度;
(4)如图2,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x>0,y<0且|x|<|y|,则x+y是( ).
A. 零B. 正数C. 负数D. 非负数
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子计算正确的是( )
A.x+x2=x3
B.3x2﹣2x=x
C.(3x2y)2=3x4y2
D.(﹣3x2y)2=9x4y2 -
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法对31500取近似数,并精确到千位,用科学计数法可表示为 .
相关试题

