搜索
【题目】如图，二次函数y1=ax2+bx+3的图像与x轴相交于点A（﹣3，0）、B（1，0），交y轴于点C，C，D是二次函数图像上的一对对称点，一次函数y2=mx+n的图像经过B、D两点． 
（1）求二次函数的解析式及点D的坐标；
（2）根据图像写出y2＞y1时，x的取值范围．
参考答案：
【答案】
（1）解：二次函数y1=ax2+bx+3的图像经过点A（﹣3，0），B（1，0）；
∴ 
，
解得 
；
∴二次函数图像的解析式为y1=﹣x2﹣2x+3；
∴点D的坐标为（﹣2，3）
（2）解：y2＞y1时，x的取值范围是x＜﹣2或x＞1
【解析】（1）将A、B的坐标代入抛物线的解析式中即可求得待定系数的值，进而可根据抛物线的对称轴求出D点的坐标；（2）联立两函数的解析式，即可求得B、D的坐标，进而可判断出y2＞y1时x的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，四边形OABC四个顶点的坐标分别为O（0，0），A（﹣3，0），B（﹣4，2），C（﹣1，2）．将四边形OABC绕点O顺时针旋转90°后，点A，B，C分别落在点A′，B′，C′处．
（1）请你在所给的直角坐标系中画出旋转后的四边形OA′B′C′；
（2）点C旋转到点C′所经过的弧的半径是 ， 点C经过的路线长是 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，已知AB是圆O的直径，圆O过BC的中点D，且DE⊥AC．
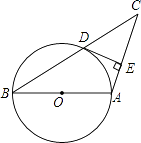
（1）求证：DE是圆O的切线；
（2）若∠C=30°，CD=10cm，求圆O的半径． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知数轴上两点A，B对应的数分别为﹣1、3，点P为数轴上一动点．
（1）若点P到点A、点B的距离相等，写出点P对应的数 ；
（2）若点P到点A，B的距离之和为6，那么点P对应的数 ；
（3）点A，B分别以2个单位长度/分、1个单位长度/分的速度向右运动，同时P点以6个单位长度/分的速度从O点向左运动．当遇到A时，点P立刻以同样的速度向右运动，并不停地往返于点A与点B之间，求当点A与点B重合时，点P所经过的总路程是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】A，B两地相距2400米，甲、乙两人分别从A，B两地同时出发相向而行，乙的速度是甲的2倍，已知乙到达A地15分钟后甲到达B地．
（1）求甲每分钟走多少米？
（2）两人出发多少分钟后恰好相距480米？
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：
如图1，在平面直角坐标系xOy中，直线y1=ax+b与双曲线y2=
交于A（1，3）和B（﹣3，﹣1）两点．
观察图像可知：
①当x=﹣3或1时，y1=y2；
②当﹣3＜x＜0或x＞1时，y1＞y2 ， 即通过观察函数的图像，可以得到不等式ax+b＞ 的解集．
有这样一个问题：求不等式x3+4x2﹣x﹣4＞0的解集．
某同学根据学习以上知识的经验，对求不等式x3+4x2﹣x﹣4＞0的解集进行了探究．
下面是他的探究过程，请将（1）、（2）、（3）补充完整：
（1）①将不等式按条件进行转化：
当x=0时，原不等式不成立；
当x＞0时，原不等式可以转化为x2+4x﹣1＞
；
当x＜0时，原不等式可以转化为x2+4x﹣1＜；
②构造函数，画出图像
设y3=x2+4x﹣1，y4= ， 在同一坐标系中分别画出这两个函数的图像．
双曲线y4=如图2所示，请在此坐标系中画出抛物线y3=x2+4x﹣1；（不用列表）
（2）确定两个函数图像公共点的横坐标
观察所画两个函数的图像，猜想并通过代入函数解析式验证可知：满足y3=y4的所有x的值为
（3）借助图像，写出解集
结合（1）的讨论结果，观察两个函数的图像可知：不等式x3+4x2﹣x﹣4＞0的解集为 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，AD平分∠BAC，DE∥AC交AB于E，DF∥AB交AC于F，若AF=6，则四边形AEDF的周长是（ ）
A. 24 B. 28 C. 32 D. 36
相关试题
