【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 4 |
第2组 | 30≤x<35 | 8 |
第3组 | 35≤x<40 | 16 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
请结合图表完成下列各题: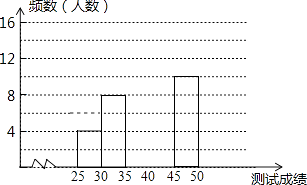
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
(4)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小宇与小强两名男同学能分在同一组的概率.
参考答案:
【答案】
(1)解:表中a的值是:
a=50﹣4﹣8﹣16﹣10=12
(2)解:根据题意画图如下:

(3)解:本次测试的优秀率是 ![]() =0.44.
=0.44.
答:本次测试的优秀率是0.44
(4)解:用A表示小宇,B表示小强,C、D表示其他两名同学,根据题意画树状图如下:
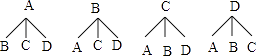
共有12种情况,小宇与小强两名男同学分在同一组的情况有2种,
则小宇与小强两名男同学分在同一组的概率是 ![]()
【解析】(1)用总人数减去第1、2、3、5组的人数,即可求出a的值;(2)根据(1)得出的a的值,补全统计图;(3)用成绩不低于40分的频数乘以总数,即可得出本次测试的优秀率;(4)用A表示小宇,B表示小强,C、D表示其他两名同学,画出树状图,再根据概率公式列式计算即可.
【考点精析】解答此题的关键在于理解频数分布直方图的相关知识,掌握特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图),以及对列表法与树状图法的理解,了解当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.

(1)求证:△ABE≌△CDF;
(2)若AB=DB,猜想:四边形DFBE是什么特殊的四边形?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=kx﹣1(k>0)的图象与BC边交于点E.当F为AB的中点时,求该函数的解析式.
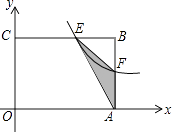
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市公交公司为应对春运期间的人流高峰,计划购买A、B两种型号的公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车3辆,共需650万元,
(1)试问该公交公司计划购买A型和B型公交车每辆各需多少万元?
(2)若该公司预计在某条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用W不超过1200万元,且确保这10辆公交车在某条线路的年均载客量总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案的总费用W最少?最少总费用是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种型号热水器的容量为180升,设其工作时间为y分,每分的排水量为x升.
(1)写出y关于x的函数表达式和自变量x的取值范围;
(2)当每分钟的排水量为10升时,热水器工作多长时间?
(3)如果热水器可连续工作的时间不超过1小时,那么每分的排水量应控制在什么范围内?
-
科目: 来源: 题型:
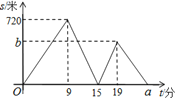
查看答案和解析>>【题目】小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s (米)与小明出发时间t (分)之间的函数关系如图所示.下列说法:
①小华先到达青少年宫;②小华的速度是小明速度的2.5倍;③a=24;④b=480.其中正确的是( )
A.
 B.
B.  C.
C. 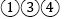 D.
D. 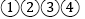
-
科目: 来源: 题型:
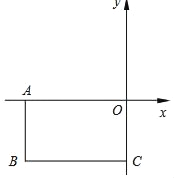
查看答案和解析>>【题目】长方形OABC,O为平面直角坐标系的原点,OA=5,OC=3,点B在第三象限.
(1)求点B的坐标;
(2)如图,若过点B的直线BP与长方形OABC的边交于点P,且将长方形OABC的面积分为1:4两部分,求点P的坐标.
相关试题

