【题目】如图Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,再添两个条件不能够全等的是( )

A.AB=A′B′,BC=B′C′B.AC=AC′,BC=BC′
C.∠A=∠A′,BC=B′C′D.∠A=∠A′,∠B=∠B′
参考答案:
【答案】D
【解析】
解答此题的关键是要熟练掌握直角三角形全等的判定方法,然后逐项分析即可得出答案.
解:A选项,AB=A′B′,BC=B′C′,
可利用HL 判定Rt△ABC≌Rt△A′B′C′,
同理B选项,也可利用HL 判定Rt△ABC≌Rt△A′B′C′,
C选项∠A=∠A′,BC=B′C′,可利用AAS判定Rt△ABC≌Rt△A′B′C′,
D选项,∠A=∠A′,∠B=∠B′,只能证明Rt△ABC∽Rt△A′B′C′,
不能证明Rt△ABC≌Rt△A′B′C′.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究:如图①,△ABC是等边三角形,在边AB、BC的延长线上截取BM=CN,连结MC、AN,延长MC交AN于点P.
(1)求证:△ACN≌△CBM;
(2)∠CPN= °;(给出求解过程)
(3)应用:将图①的△ABC分别改为正方形ABCD和正五边形ABCDE,如图②、③,在边AB、BC的延长线上截取BM=CN,连结MC、DN,延长MC交DN于点P,则图②中∠CPN= °;(直接写出答案)
(4)图③中∠CPN= °;(直接写出答案)
(5)拓展:若将图①的△ABC改为正n边形,其它条件不变,则∠CPN= °(用含n的代数式表示,直接写出答案).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三边分别为a、b、c,则下列条件中不能判定△ABC是直角三角形的是( )
A. b2=a2﹣c2B. a:b:c=1:
 :2
:2C. ∠C=∠A﹣∠BD. ∠A:∠B:∠C=3:4:5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为4,⊙B的半径为2,点P是⊙B上的一个动点,则PD﹣
 PC的最大值为_____.
PC的最大值为_____.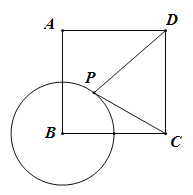
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB、AC边上的高CE、BD相交于点P,图中与△BPE相似的三角形共有( )
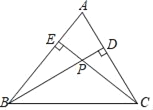
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为24米.要围成的菜园是如图所示的矩形ABCD.设BC边的长为x米,AB边的长为y米,则y与x之间的函数关系式是( )

A. y=-2x+24(0<x<12) B. y=-
 x+12(0<x<24)
x+12(0<x<24)C. y=2x-24(0<x<12) D. y=
 x-12(0<x<24)
x-12(0<x<24) -
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为( )
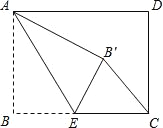
A. 3 B.
 C. 2或3 D. 3或
C. 2或3 D. 3或
相关试题

