搜索
【题目】将一根24cm的筷子，置于底面直径为15cm，高8cm的圆柱形水杯中，如图所示，设筷子露在杯子外面的长度hcm，则h的取值范围是（ ） 
A.h≤17cm
B.h≥8cm
C.15cm≤h≤16cm
D.7cm≤h≤16cm
参考答案：
【答案】D
【解析】解：如图，当筷子的底端在D点时，筷子露在杯子外面的长度最长， ∴h=24﹣8=16cm；
当筷子的底端在A点时，筷子露在杯子外面的长度最短，
在Rt△ABD中，AD=15，BD=8，∴AB= 
=17，
∴此时h=24﹣17=7cm，
所以h的取值范围是7cm≤h≤16cm．
故选D．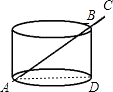
当筷子的底端在A点时，筷子露在杯子外面的长度最短；当筷子的底端在D点时，筷子露在杯子外面的长度最长．然后分别利用已知条件根据勾股定理即可求出h的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】美国NBA篮球职业联赛冠军队某投球手罚球时，“三投都不中”这一事件是（ ）
A.不可能事件B.必然事件C.随机事件D.无法确定
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读与应用：阅读1：a、b为实数，且a＞0，b＞0，因为
，所以
从而
（当a=b时取等号）．阅读2：若函数
；（m＞0，x＞0，m为常数），由阅读1结论可知：
，所以当
，即
时，函数的最小值为
．阅读理解上述内容，解答下列问题：
问题1：已知一个矩形的面积为4，其中一边长为x，则另一边长为
，周长为2（
），求当x= 时，周长的最小值为 ；问题2：已知函数
（
）与函数
（），当x= 时，
的最小值为 ；问题3：某民办学校每天的支出总费用包含以下三个部分：一是教职工工资4900元；二是学生生活费成本每人10元；三是其他费用．其中，其他费用与学生人数的平方成正比，比例系数为0.01．当学校学生人数为多少时，该校每天生均投入最低？最低费用是多少元？（生均投入=支出总费用÷学生人数）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC为等边三角形，点D、E分别在BC、AC边上，且AE=CD，AD与BE相交于点F．
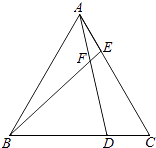
（1）求证：△ABE≌△CAD；
（2）求∠BFD的度数． -
科目： 来源： 题型：
查看答案和解析>>【题目】相反数等于－5的数是（ ）
A.5
B.－5
C.5或－5
D.不能确定 -
科目： 来源： 题型：
查看答案和解析>>【题目】点A（0，5）关于原点对称，得到点A′，那么A′的坐标是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解抛物线
上任意一点到点（0，1）的距离与到直线y=﹣1的距离相等，你可以利用这一性质解决问题．问题解决
如图，在平面直角坐标系中，直线
与y轴交于C点，与函数的图象交于A，B两点，分别过A，B两点作直线y=﹣1的垂线，交于E，F两点．（1）写出点C的坐标，并说明∠ECF=90°；
（2）在△PEF中，M为EF中点，P为动点．
①求证：
；②已知PE=PF=3，以EF为一条对角线作平行四边形CEDF，若1＜PD＜2，试求CP的取值范围．
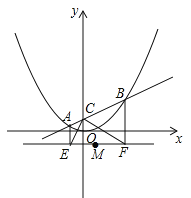
相关试题
