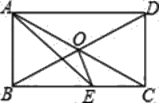
【题目】如图,在矩形ABCD中,∠BAD的平分线交BC于点E,O为对角线AC、BD的交点,且∠CAE=15° .
(1)求证:△AOB为等边三角形;
(2)求∠BOE度数.
参考答案:
【答案】(1)见解析;(2)75°
【解析】试题分析:(1)因为四边形ABCD是矩形,所以OA=OB,则只需求得∠BAC=60°,即可证明三角形是等边三角形;
(2)因为∠B=90°,∠BAE=45°,所以AB=BE,又因为△ABO是等边三角形,则∠OBE=30°,故∠BOE度数可求.
(1)证明:∵四边形ABCD是矩形
∴∠BAD=∠ABC=90°,AO=BO=AC=BD
∵AE是∠BAD的角平分线;
∴∠BAE=45°
∵∠CAE=15°
∴∠BAC=60°
∴△AOB是等边三角形;
(2)解:∵在Rt△ABE中,∠BAE=45°
∴AB=BE
∵△ABO是等边三角形
∴AB=BO
∴OB=BE
∵∠OBE=30°,OB=BE,
∴∠BOE=(180°﹣30°)=75°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,不正确的是( )
A.一次函数不一定是正比例函数
B.正比例函数是一次函数的特例
C.不是正比例函数就不是一次函数
D.不是一次函数就不是正比例函数 -
科目: 来源: 题型:
查看答案和解析>>【题目】把3个长为a,宽为b(a>b)的长方形如图放置,恰好拼成一个大长方形,

(1)大长方形的面积S=____________(用含字母a、b的代数式表示);
(2)a、b之间的等量关系是:__________________;
(3)当b=2时,面积S=?b=3时,周长C=?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品的进价为40元,在某段时间内若以每件x元出售,可卖出(100﹣x)件,当x=____时才能使利润最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角尺按如图方式进行摆放,∠1、∠2不一定互补的是( )
A.
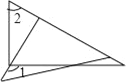 B.
B. 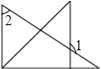
C.
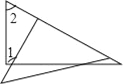 D.
D. 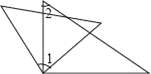
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣2x﹣3与x轴的交点坐标为
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品进货单价为30元,按40元一个销售能卖40个;若销售单价每涨1元,则销量减少1个.为了获得最大利润,此商品的最佳售价应为元.
相关试题

