【题目】如图是小明利用等腰直角三角板测量旗杆高度的示意图.等腰直角三角板的斜边BD与地面AF平行,当小明的视线恰好沿BC经过旗杆顶部点E时,测量出此时他所在的位置点A与旗杆底部点F的距离为10米.如果小明的眼睛距离地面1.7米,那么旗杆EF的高度为( )

A. 10米 B. 11.7米 C. 10![]() 米 D. (5
米 D. (5![]() +1.7)米
+1.7)米
参考答案:
【答案】B
【解析】
延长BD交EF于H,如图,利用四边形ABHF为矩形得到AF=BH=10,HF=AB=1.7,再利用△BCD为等腰直角三角形,可判断△BHE为等腰直角三角形,所以EH=BH=10,然后计算EH+HF即可.
延长BD交EF于H,如图,
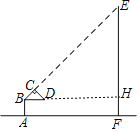
∵BD∥AF,EF⊥AF,
∴BH⊥EF,
易得四边形ABHF为矩形,
∴AF=BH=10,HF=AB=1.7,
∵△BCD为等腰直角三角形,
∴∠CBD=45°,
∴△BHE为等腰直角三角形,
∴EH=BH=10,
∴EF=EH+HF=10+1.7=11.7.
答:旗杆EF的高度为11.7m.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题.

(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用直尺和圆规作一个角∠A′O′B′,等于已知角∠AOB,能得出∠A′O′B′=∠AOB的依据是( )

A.SASB.ASAC.AASD.SSS
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
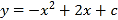 与x轴交于A,B两点,它们的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.已知点A的坐标为(﹣1,0).
与x轴交于A,B两点,它们的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.已知点A的坐标为(﹣1,0).(1)求该抛物线的解析式及顶点M的坐标;
(2)求△EMF与△BNF的面积之比.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为等边△ABC的高,E、F分别为线段AD、AC上的动点,且AE=CF,当BF+CE取得最小值时,∠AFB=( )

A. 112.5°B. 105°C. 90°D. 82.5°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊿
 中,
中, ,点
,点 分别在
分别在 边上,且
边上,且 ,
,  .
.⑴.求证:⊿
 是等腰三角形;
是等腰三角形;⑵.当
 时,求
时,求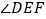 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为适应新中考英语听说机考,九年级甲、乙两位同学使用某手机软件进行英语听说练习并记录了40次的练习成绩.甲、乙两位同学的练习成绩统计结果如图所示:

下列说法正确的是( )
A. 甲同学的练习成绩的中位数是38分
B. 乙同学的练习成绩的众数是15分
C. 甲同学的练习成绩比乙同学的练习成绩更稳定
D. 甲同学的练习总成绩比乙同学的练习总成绩低
相关试题

