【题目】探究题
(1)【问题探究】
如图1,DF∥CE,∠PCE=∠α,∠PDF=∠β,猜想∠DPC与α、β之间有何数量关系?并说明理由;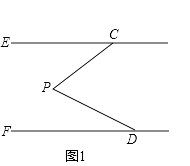
(2)【问题迁移】
如图2,DF∥CE,点P在三角板AB边上滑动,∠PCE=∠α,∠PDF=∠β.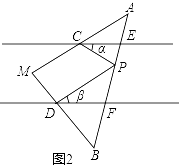
①当点P在E、F两点之间运动时,如果α=30°,β=40°,则∠DPC=°.
②如果点P在E、F两点外侧运动时(点P与点A、B、E、F四点不重合),写出∠DPC与α、β之间的数量关系,并说明理由.
参考答案:
【答案】
(1)
∠DPC=α+β.
理由:如图,延长CP交DF于A,
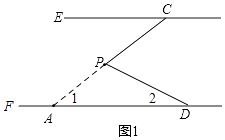
∵DF∥CE,
∴∠PCE=∠1=α,
∵∠DPC=∠2+∠1=180°﹣∠APD,
∴∠DPC=∠2+∠PCE=α+β;
(2)① 70
②如图,∠DPC=β﹣α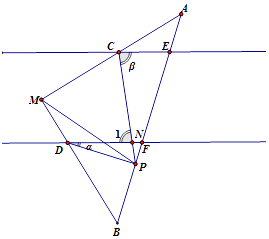
∵DF∥CE,
∴∠PCE=∠1=β,
∵∠DPC=∠1﹣∠FDP=∠1﹣α.
∴∠DPC=β﹣α;
如图,∠DPC=α﹣β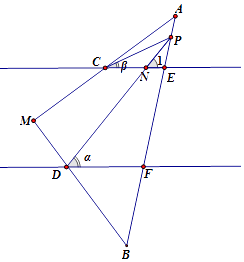
∵DF∥CE,
∴∠PDF=∠1=α,
∵∠DPC=∠1﹣∠ACE=∠1﹣β.
∴∠DPC=α﹣β.
【解析】(1)【问题探究】延长CP交DF于A,根据平行线的性质以及三角形外角性质进行计算即可;(2)【问题迁移】①延长CP交DF于G,根据平行线的性质以及三角形外角性质进行计算即可;②分两种情况进行讨论:点P在BF上,点P在AE上,分别根据平行线的性质以及三角形外角性质进行计算即可.
【问题迁移】(2)如图2,延长CP交DF于G,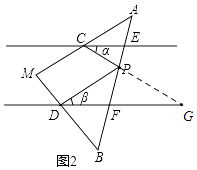
∵DF∥CE,
∴∠PCE=∠G=30°,
∴∠DPC=∠G+∠GDP=30°+40°=70°,
故答案为:70;
-
科目: 来源: 题型:
查看答案和解析>>【题目】节约是一种美德,节约是一种智慧.据不完全统计,全国每年浪费食物总量折合粮食可养活约3亿5千万人,350000000用科学记数法表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等式(x-2019)0=1成立,则x的取值范围是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索题:图a是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.
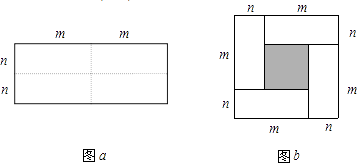
(1)请用两种不同的方法,求图b中阴影部分的面积:方法1:; 方法2:;
(2)观察图b,写出代数式(m+n)2 , (m﹣n)2 , mn之间的等量关系,并通过计算验证;
(3)根据(2)题中的等量关系,解决如下问题:若2a+b=5,ab=2,求(2a﹣b)2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣2x﹣3的顶点坐标是( )
A.(﹣1,﹣4)B.(3,0)C.(2,﹣3)D.(1,﹣4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若方程﹣(m+3)x|m|﹣2﹣5=0是关于x的一元一次方程,则m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若﹣2ax﹣3b3与5ab2y﹣1是同类项,则x+y= .
相关试题

