【题目】每年的3月22日为联合国确定的“世界水日”,某社区为了宣传节约用水,从本社区1000户家庭中随机抽取部分家庭,调查他们每月的用水量,并将调查的结果绘制成如下两幅尚不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题:
(1)此次抽样调查的样本容量是 ;
(2)补全频数分布直方图,求扇形图中“6吨﹣﹣9吨”部分的圆心角的度数;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社会用户中约有多少户家庭能够全部享受基本价格?

参考答案:
【答案】(1)100;(2)补图见解析;(3)680户.
【解析】分析:(1)由3~6吨的户数及其百分比可得样本容量;
(2)总户数减去其他分组的户数之和求得6~9吨的户数,即可补全直方图,用6~9吨的户数所占比例乘以360度可得圆心角度数;
(3)总户数乘以样本中3~12吨的户数所占比例即可得.
详解:(1)此次抽样调查的样本容量是10÷10%=100,
故答案为:100;
(2)6~9吨的户数为100﹣(10+38+24+8)=20(户),
补全频数分布直方图如下:
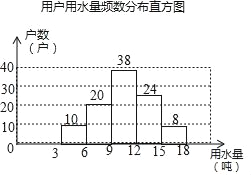
扇形图中“6吨﹣﹣9吨”部分的圆心角的度数为360°×![]() =72°;
=72°;
(3)1000×![]() =680,
=680,
答:该社区约有680户家庭的用水全部享受基本价格.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,AD是△ABC的中线,将BC边所在直线绕点D顺时针旋转
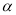 角,交边AB于点M,交射线AC于点N,设AM=xAB,AN=yAC(x,y≠0).
角,交边AB于点M,交射线AC于点N,设AM=xAB,AN=yAC(x,y≠0).(1)如图1,当△
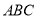 为等边三角形且
为等边三角形且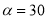 °时,证明:△AMN∽△DMA;
°时,证明:△AMN∽△DMA;(2)如图2,证明:
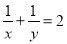 ;
;(3)如图3,当G是AD上任意一点时(点G不与A重合),过点G的直线交边AB于点
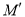 ,交射线AC于点
,交射线AC于点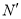 ,设AG=nAD,
,设AG=nAD, 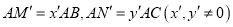 ,猜想:
,猜想: 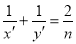 是否成立?并说明理由.
是否成立?并说明理由.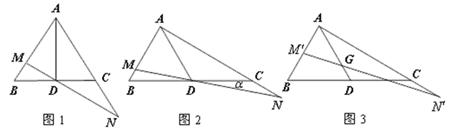
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,矩形ABCD的边AD在y轴上,抛物线
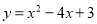 经过点A、点B,与x轴交于点E、点F,且其顶点M在CD上。
经过点A、点B,与x轴交于点E、点F,且其顶点M在CD上。(1)请直接写出下列各点的坐标:
A ,B ,C ,D ;
(2)若点P是抛物线上一动点(点P不与点A、点B重合),过点P作
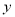 轴的平行线l与直线AB交于点G,与直线BD交于点H,如图2。
轴的平行线l与直线AB交于点G,与直线BD交于点H,如图2。①当线段PH=2GH时,求点P的坐标;
②当点P在直线BD下方时,点K在直线BD上,且满足△KPH∽△AEF,求△KPH面积的最大值。
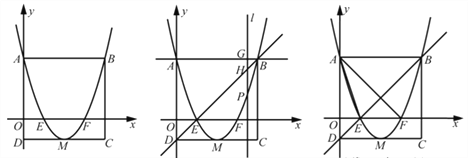
图1 图2 备用图
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,在平面直角坐标系中,点A,B,C都在坐标轴上,且OA=OB=OC,△ABC的面积为9,点P从C点出发沿y轴负方向以1个单位/秒的速度向下运动,连接PA,PB,D(﹣m,﹣m)为AC上的点(m>0)
(1)试分别求出A,B,C三点的坐标;
(2)设点P运动的时间为t秒,问:当t为何值时,DP与DB垂直且相等?请说明理由;
(3)如图2,若PA=AB,在第四象限内有一动点Q,连QA,QB,QP,且∠PQA=60°,当Q在第四象限内运动时,求∠APQ与∠PBQ的度数和.
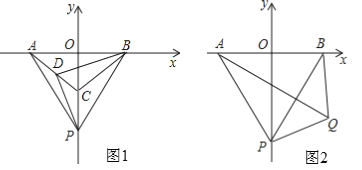
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AB∥CD,AD⊥AB,∠B=60°,AB=10,BC=4,点P沿线段AB从点A向点B运动,设AP=x.

(1)求AD的长;
(2)点P在运动过程中,是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似?若存在,求出x的值;若不存在,请说明理由;
(3)设△ADP与△PCB的外接圆的面积分别为S1、S2,若S=S1+S2,求S的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,则a,b满足的关系是

A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,O为坐标原点,已知A(-1,1),在坐标轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( )
A. 10个 B. 8个 C. 4个 D. 6个
相关试题

