Question

【题目】在平面直角坐标系中，已知直线AB 与y轴交于点A，与x轴交于点B，与双曲线y= （x＞0）交于点C（1，6）和点D（3，n）．作CE⊥y轴于E，DF⊥x轴于F．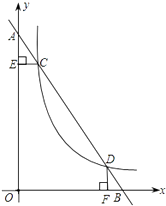

（1）求出m、n的值；
（2）求出直线AB的解析式；
（3）是否有△AEC≌△DFB，并说明理由．

Answer 1

【答案】
（1）

解：∵点C（1，6）和点D（3，n），

∴依题意得：m=6×1=6，

则n= =2，

故m=6，n=2

（2）

解：设直线AB的函数解析式为y=kx+b（k≠0）

由题意得 ，

解得： ．

故直线AB的解析式为y=﹣2x+8

（3）

解：有△AEC≌△DFB，理由如下：

∵y=﹣2x+8

当x=0时，y=8；

当y=0时，﹣2x+8=0，

解得：x=4；

∴A（0，8），B （4，0），

∵CE⊥y轴于E，DF⊥x轴于F，

∴∠AEC=∠DFB=90°

∵A（0，8），B （4，0）C（1，6），D（3，2），

∴AE=8﹣6=2，DF=2，CE=1，BF=4﹣3=1，

∴AE=DF，CE=BF，

在△AEC和△DFB中，

，

∴△AEC≌△DFB（SAS）．

【解析】（1）直接将C点坐标代入反比例函数解析式，进而得出m的值，进而求出n的值；（2）直接利用待定系数法求出直线AB的解析式；（3）利用已知解析式求出AE=DF，CE=BF，进而利用全等三角形的判定得出答案．