【题目】已知甲加工A型零件60个所用时间和乙加工B型零件80个所用时间相同,甲、乙两人每天共加工35个零件,设甲每天加工x个A型零件.
(1)求甲、乙每天各加工零件多少个?
(2)根据市场预测,加工A型零件所获得的利润为m元/件(3≤m≤5),加工B型零件所获得的利润每件比A型少1元.求甲、乙每天加工的零件所获得的总利润P(元)与m的函数关系式,并求P的最大值和最小值.
参考答案:
【答案】
(1)解:设甲每天加工x个A型零件,则乙每天加工(35﹣x)个B型零件,根据题意,
易得 ![]() =
= ![]() ,
,
解得x=15,
经检验,x=15是原方程的解,且符合题意.
35﹣15=20(个).
答:甲每天加工15个A型零件,则乙每天加工20个B型零件
(2)解:P=15m+20(m﹣1),
即P=35m﹣20,
∵在P=35m﹣20中,P是m的一次函数,k=35>0,P随m的增大而增大,
又由已知得:3≤m≤5,
∴当m=5时,P的最大值=155,
当m=3时,P的最小值=85
【解析】(1)设甲每天加工x个A型零件,则乙每天加工(35﹣x)个B型零件,根据题意,易得 ![]() =
= ![]() ,解方程可得x的值,进而可得答案;(2)根据题意,可得关系式P=15m+20(m﹣1),化简可得P=35m﹣20,根据一次函数的性质分析可得答案.
,解方程可得x的值,进而可得答案;(2)根据题意,可得关系式P=15m+20(m﹣1),化简可得P=35m﹣20,根据一次函数的性质分析可得答案.
【考点精析】关于本题考查的分式方程的应用,需要了解列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位)才能得出正确答案.
-
科目: 来源: 题型:
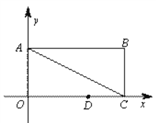
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=1,OC=2,点D在边OC上且OD=1.25.
(1)求直线AC的解析式.
(2)在y轴上是否存在点P,直线PD与矩形对角线AC交于点M,使得△DMC为等腰三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)抛物线y=-x2经过怎样平移,才能使得平移后的抛物线过点D和点E(点E在y轴正半轴上),且△ODE沿DE折叠后点O落在边AB上O/处?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(
 ﹣
﹣ 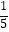 )×(
)×( 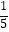 )﹣2÷|﹣
)﹣2÷|﹣  |+(﹣
|+(﹣ 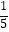 )0+(﹣0.25)2007×42007 .
)0+(﹣0.25)2007×42007 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是2015年12月月历.
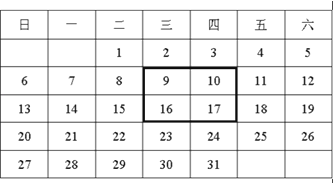
(1)如图,用一正方形框在表中任意框住4个数,记左上角的一个数为x,则另三个数用含x的式子表示出来,从小到大依次是 , , .
(2)在表中框住四个数之和最小记为a1,和最大记为a2,则a1+a2= .
(3)当(1)中被框住的4个数之和等于76时,x的值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】按下面的程序计算:当输入x=100 时,输出结果是299;当输入x=50时,输出结果是446;如果输入 x 的值是正整数,输出结果是257,那么满足条件的x的值最多有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,延长平行四边形ABCD的边DC到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.
(1)求证:BF=CF;
(2)若AB=2,AD=4,且∠AFC=2∠D,求平行四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知直线AB 与y轴交于点A,与x轴交于点B,与双曲线y=
 (x>0)交于点C(1,6)和点D(3,n).作CE⊥y轴于E,DF⊥x轴于F.
(x>0)交于点C(1,6)和点D(3,n).作CE⊥y轴于E,DF⊥x轴于F.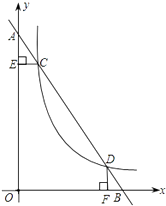
(1)求出m、n的值;
(2)求出直线AB的解析式;
(3)是否有△AEC≌△DFB,并说明理由.
相关试题

