【题目】甲乙两人玩摸球游戏:一个不透明的袋子中装有相同大小的3个球,球上分别标有数字1,2,3.首先,甲从中随机摸出一个球,然后,乙从剩下的球中随机摸出一个球,比较球上的数字,较大的获胜.
(1)求甲摸到标有数字3的球的概率;
(2)这个游戏公平吗?请说明理由.
参考答案:
【答案】
(1)解:∵袋子中装有相同大小的3个球,球上分别标有数字1,2,3,
∴甲摸到标有数字3的球的概率为 ![]()
(2)解:解:游戏公平,理由如下:
列举所有可能:
甲 乙 | 1 | 2 | 3 |
1 | 3 | 1 | |
2 | 3 | 2 | |
3 | 2 | 1 |
由表可知甲获胜的概率= ![]() ,乙获胜的概率=
,乙获胜的概率= ![]() ,
,
所以游戏是公平的.
【解析】(1)由袋子中装有相同大小的3个球,球上分别标有数字1,2,3,所以甲摸到标有数字3的球的概率为![]() ;(2)列表得到所有可能,甲获胜的概率=
;(2)列表得到所有可能,甲获胜的概率=![]() ,乙获胜的概率=
,乙获胜的概率=![]() ,所以游戏是公平的.
,所以游戏是公平的.![]()
【考点精析】认真审题,首先需要了解概率公式(一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n).
-
科目: 来源: 题型:
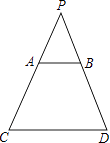
查看答案和解析>>【题目】如图,光源P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,点P到CD的距离是2.7m,则点P到AB间的距离是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD与正方形EFGH是位似形,已知A(0,5),D(0,3),E(0,1),H(0,4),则位似中心的坐标是 .
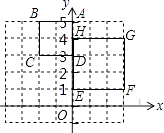
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请在图中标明旋转中心P的位置并写出其坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
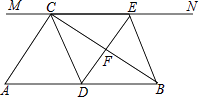
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中:①
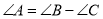 ,②
,②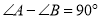 ,③
,③ ,④
,④ 中,能确定
中,能确定 是直角三角形的条件有( )
是直角三角形的条件有( )A.1个B.2个C.3个D.4个
相关试题

