Question

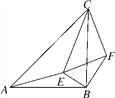
【题目】如图，△ABC和△CEF均为等腰直角三角形，E在△ABC内，∠CAE＋∠CBE＝90°，连接BF.

(1)求证：△CAE∽△CBF；

(2)若BE＝1，AE＝2，求CE的长．

Answer 1

【答案】（1）见解析 （2）

证明：∵△ABC和△CEF均为等腰直角三角形，∴，∠ACB＝∠ECF＝45°

∵∠ACB＝∠ACE＋∠BCE，∠ECF＝∠BCF＋∠BCE，∴∠ACE＝∠BCF，∴△CAE∽△CBF.

(2)解：由(1)可知△CAE∽△CBF，∴∠CAE＝∠CBF，.又∵AE＝2，∴＝，∴BF＝∵∠CAE＋∠CBE＝90°，

∴∠CBF＋∠CBE＝90°，

∴∠EBF＝90°，

∴EF2＝BE2＋BF2＝12＋()2＝3，

∴EF＝，∴CE＝EF＝.

【解析】试题分析：首先由△ABC和△CEF均为等腰直角三角形可得∠ACB＝∠ECF＝45°.然后根据相似三角形判定的方法，推得△CAE∽△CBF即可.

首先根据△CAE∽△CBF，判断出∠CAE＝∠CBF,再根据 判断出,然后在中，根据勾股定理，求出的长度，再根据 的关系，求出的长即可．

试题解析：∵△ABC和△CEF均为等腰直角三角形，

∠ACB＝∠ECF＝45°.

∵∠ACB＝∠ACE＋∠BCE，∠ECF＝∠BCF＋∠BCE，

∴∠ACE＝∠BCF，

∴△CAE∽△CBF.

(2)由(1)可知△CAE∽△CBF，

∴∠CAE＝∠CBF，

又∵AE＝2，

∵∠CAE＋∠CBE＝90°，

∴∠CBF＋∠CBE＝90°，

∴∠EBF＝90°，