【题目】已知关于x的方程x2﹣2(m+1)x+m2=0
(1)当m取何值时,方程有两个相等的实数根;
(2)为m选取一个合适的整数,使方程有两个不相等的实数根,并求出这两个根.
参考答案:
【答案】(1)当m=﹣0.5时,方程有两个相等的实数根;(2)选取m=0, x1=0,x2=2.(答案不唯一).
【解析】试题分析:(1)方程有两个相等的实数根,必须满足△=b2-4ac=0,从而建立关于m的方程,解方程求出m的值即可;
(2)答案不唯一,方程有两个不相等的实数根,即△>0,可以解得m>-![]() ,在m>-
,在m>-![]() 的范围内选取一个合适的整数求解即可.
的范围内选取一个合适的整数求解即可.
试题解析:(1)由题意知:△=b2﹣4ac=[﹣2(m+1)]2﹣4m2=[﹣2(m+1)+2m][﹣2(m+1)﹣2m]=﹣2(﹣4m﹣2)=8m+4=0,
解得m=﹣0.5,
∴当m=﹣0.5时,方程有两个相等的实数根;
(2)方程有两个不相等的实数根,即△=8m+4>0,可以解得m>﹣![]() ,
,
选取m=0,(答案不唯一,注意开放性)
方程为x2﹣2x=0,
解得x1=0,x2=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察图形,解答问题:

(1)按下表已填写的形式填写表中的空格:
图①
图②
图③
三个角上三个数的积
1×(-1)×2=-2
(-3)×(-4)×(-5)=-60
三个角上三个数的和
1+(-1)+2=2
(-3)+(-4)+(-5)=-12
积与和的商
(-2)÷2=-1
(2)请用你发现的规律求出图④中的数x和图⑤中的数y.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某自行车厂一周计划生产
 辆自行车,平均每天生产
辆自行车,平均每天生产 辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正,减产为负);
辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正,减产为负);星期
一
二
三
四
五
六
日
增减
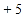





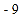
 根据记录可知前三天共生产________辆;
根据记录可知前三天共生产________辆; 产量最多的一天比产量最少的一天多生产________辆;
产量最多的一天比产量最少的一天多生产________辆; 该厂实行计件工资制,每辆车
该厂实行计件工资制,每辆车 元,超额完成任务每辆奖
元,超额完成任务每辆奖 元,少生产一辆扣
元,少生产一辆扣 元,那么该厂工人这一周的工资总额是多少?
元,那么该厂工人这一周的工资总额是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P为函数y=
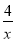 (x>0)图象上一点过点P作x轴、y轴的平行线,分别与函数y
(x>0)图象上一点过点P作x轴、y轴的平行线,分别与函数y (x>0)的图象交于点A,B,则△AOB的面积为_____.
(x>0)的图象交于点A,B,则△AOB的面积为_____.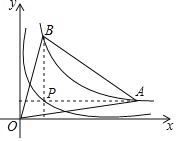
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学完“有理数的运算”后,某中学七年级各班各选出5名学生组成一个代表队,在数学方老师的组织下进行一次知识竞赛,竞赛规则是:每队都分别给出50道题,答对一题得3分,不答或答错一题倒扣1分
(1)如果2班代表队最后得分142分,那么2班代表队回答对了多少道题?
(2)1班代表队的最后得分能为145分吗?请简要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地建设一项水利工程,工程需要运送的土石方总量为360万米3.
(1)写出运输公司完成任务所需的时间y(单位:天)与平均每天的工作量x(单位:万米3)之间的函数关系式;
(2)当运输公司平均每天的工作量15万米3,完成任务所需的时间是多少?
(3)为了能在150天内完成任务,平均每天的工作量至少是多少万米3?
-
科目: 来源: 题型:
查看答案和解析>>【题目】老师在黑板上出了一道解方程的题
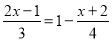 ,小明马上举手,要求到黑板上做,他是这样做的:
,小明马上举手,要求到黑板上做,他是这样做的: 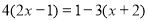 ……………… …①
……………… …①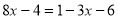 …………………… …②
…………………… …②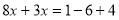 …………………… …③
…………………… …③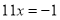 ………………………………… ④
………………………………… ④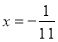 ………………………………… ⑤
………………………………… ⑤老师说:小明解一元一次方程的一般步骤都知道却没有掌握好,因此解题时有一步出现了错误,请你指出他错在 (填编号);
然后,你自己细心地解下面的方程:
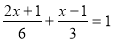 .
.
相关试题

