【题目】如图,已知AB为⊙O的直径,BD和CD为⊙O的切线,切点分别为B和C.
(1)求证:AC∥OD;
(2)当BC=BD,且BD=6cm时,求图中阴影部分的面积(结果不取近似值).

参考答案:
【答案】(1)见解析;(2)( 4π﹣3![]() )cm2.
)cm2.
【解析】分析:(1)连接OC,证明∠OCD=90°.根据切线定理得DC=DB,OB⊥BD,OC⊥CD,证得△OCD≌△OBD,再结合AB为直径,AC⊥BC,可得∠ACO=∠COM,从而得证;
(2)阴影面积=S扇形OBC-S△OBC.根据切线长定理知△BCD为等边三角形,可求∠BOC的度数,运用相关公式计算.
详解:
(1)证明:连接OC.
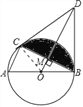
∵BD和CD为⊙O的切线,
∴DC=DB,OB⊥BD,OC⊥CD,
又OB=OC,
∴△OCD≌△OBD,
∴∠COM=∠BOM,从而易得BC⊥OD,
∵AB为直径,
∴AC⊥BC,
∴∠ACO+∠OCM=∠COM+∠OCM=90°,
∴∠ACO=∠COM,
∴AC∥OD.
(2)∵DB,DC为切线,B,C为切点,
∴DB=DC.
又∵DB=BC=6,∴△BCD为等边三角形.
∴∠BOC=360°﹣90°﹣90°﹣60°=120°,
∠OBM=90°﹣60°=30°,BM=3.
∴OM=![]() ,OB=2
,OB=2![]() .
.
∴S阴影部分=S扇形OBC﹣S△OBC=![]()
-
科目: 来源: 题型:
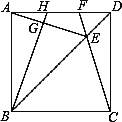
查看答案和解析>>【题目】如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=BC.连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中:
①AH=DF; ②∠AEF=45°; ③S四边形EFHG=S△DEF+S△AGH,
其中正确的结论有_____________________.(填正确的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为300,测得大楼顶端 A的仰角为450(点B,C,E在同一水平直线上)。已知AB=50m,DE=10m,求障碍物B,C两点间的距离。(结果精确到1m,参考数据:
 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A,B在数轴上分别表示有理数a,b.A,B两点之间的距离表示为AB,在数轴上A,B两点之间的距离AB=|a﹣b|.利用数形结合思想回答下列问题:
(1)数轴上表示﹣2和8两点之间的距离是________.
(2)数轴上表示x和﹣4两点A和B之间的距离表示为__________;如果AB=2,那么x=___________.
(3)若点C表示的数为x,当点C在什么位置时,|
 x+1|+|
x+1|+| x1|取得的值最小,并直接写出最小值。
x1|取得的值最小,并直接写出最小值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某公园划船项目收费标准如下:

某班18名同学一起去该公园划船,若每人划船的时间均为1小时,则租船的总费用最低为________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为进一步丰富学生课余文化生活和营造朝气蓬勃的校园文化氛围,学校组织学生开展了各种文体活动、社团活动,现在开展的社团活动有音乐,体育,美术,摄影四类,每个同学必须且只能从中选择参加一个社团,为了解学生参与社团活动的情况,学生会成员随机调查了一部分学生所参加的社团类别并绘制了以下两幅不完整的统计图,请你根据统计图提供的信息,解答下列问题:
社团活动条形统计图 社团活动扇形统计图


(1)本次一共调查了_____________________名同学;
(2)补全统计图;在扇形统计图中,“美术”所在扇形的圆心角的度数为_______________;
(3)小明和小亮都想报美术,摄影,体育社团,用画树状图或列表的方法,求他们恰好参加同一社团的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1)在RtΔABC中,∠ACB=900,∠B=600,在图中作出∠ACB的三等分线CD,CE.(要求:尺规作图,保留痕迹,不定作法)
(2)由(1)知,我们可以用尺规作出直角的三等分线,但是仅仅使用尺规却不能把任意一个角分成三等分,为此,人们发明了许多等分角的机械器具,如图(2)是用三张硬纸片自制的一个最简单的三分角器,与半圆O相接的AB带的长度与半圆的半径相等:BD带的长度任意,它的一边与直线AC形成一个直角,且志半圆相切于点B,假设需要将∠KSM三等分,如图(3),首先将角的顶点S置于BD上,角的一边SK经过点A,另一边SM与半圆相切,连接SO,则SB,SO为∠KSM的三等分线,请你证明。

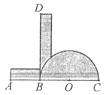

图(1) 图(2) 图(3)
相关试题

