【题目】如图,在ABCD中,E为BC边上的一点,将△ABE沿AE翻折得到△AFE,点F恰好落在线段DE上.
(1)求证:∠FAD=∠CDE
(2)当AB=5,AD=6,且tan∠ABC=2时,求线段EC的长.
参考答案:
【答案】
(1)
证明:∵四边形ABCD是平行四边形,
∴∠B=∠ADC,
∵将△BAE沿AE翻折得到△FAE,点F恰好落在线段DE上,
∴△ABE≌△AFE,
∴∠B=∠AFE,
∴∠AFE=∠ADC,
∵∠FAD=∠AFE﹣∠1,∠CDE=∠ADC﹣∠1,
∴∠FAD=∠CDE

(2)
过点D作DG⊥BE,交BE的延长线于点G.
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,CD=AB=5,
∴∠2=∠B,∠3=∠EAD,
由(1)可知,△ABE≌△AFE,
∴∠B=∠AFE,∠3=∠4,
∴∠4=∠EAD,
∴ED=AD=6,
在Rt△CDG中,tan∠2=tan∠ABC=![]() =2,
=2,
∴DG=2CG,
∵DG2+CG2=CD2,
∴(2CG)2+CG2=52,
∴CG=![]() ,DG=2
,DG=2![]() ,
,
在Rt△EDG中,
∵EG2+DG2=DE2,
∴EG=4,
∴EC=4﹣![]() .
.

【解析】(1)由平行四边形的性质和翻折的性质得出∠B=∠ADC,∠B=∠AFE,得出∠AFE=∠ADC,即可得出结论;
(2)过点D作DG⊥BE,交BE的延长线于点G.由平行四边形的性质得出∠2=∠B,∠3=∠EAD,由翻折的性质得出∠B=∠AFE,∠3=∠4,得出∠4=∠EAD.得出ED=AD=6,由三角函数得出DG=2CG,根据勾股定理得出DG2+CG2=CD2 , 求出CG、DG,再根据勾股定理求出EG,即可得出EC.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的边数恰好是从—个顶点引出的对角线条数的2倍,则此多边形的边数为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各选项中的两个图形不一定相似的是( )
A.两个正方形
B.两个等边三角形
C.各有100°角的两个等腰三角形
D.各有45°角的两个等腰三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测量山顶铁塔AE的高,小明在27m高的楼CD底部D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角36°52′.已知山高BE为56m,楼的底部D与山脚在同一水平线上,求该铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)
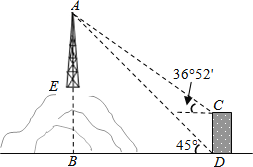
-
科目: 来源: 题型:
查看答案和解析>>【题目】张磊比小海大10岁,5年前张磊的年龄是小海的年龄的2倍,小海现在的年龄为( )
A. 10B. 15C. 20D. 25
-
科目: 来源: 题型:
查看答案和解析>>【题目】过四边形的一个顶点可以把四边形分成两个三角形;过五边形或六边形的一个顶点的对角线,可以分别把它们分成____________个三角形;过n边形的一个顶点的对角线可以把n边形分成_________个(用含n的代数式表示)三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A表示小雨家,点B表示小樱家,点C表示小丽家,她们三家恰好组成一个直角三角形,其中AC⊥BC,AC=900米,BC=1200米,AB=1500米.
(1)试说出小雨家到街道BC的距离以及小樱家到街道AC的距离.
(2)画出表示小丽家到街道AB距离的线段.
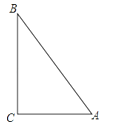
相关试题

