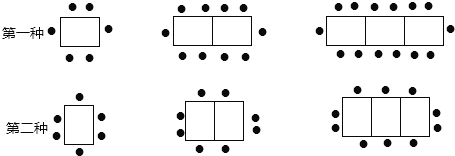
【题目】某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)有4张桌子,用第一种摆设方式,可以坐 人;用第二种摆设方式,可以坐 人;
(2)当有n张桌子时,用第一种摆设方式,可以坐 人;用第二种摆设方式,可以坐 人
(用含有n的代数式表示);
(3)一天中午,餐厅要接待85为顾客共同就餐,但餐厅中只有20张这样的长方形桌子可用,且每4张拼成一张大桌子,若你是这家餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?
参考答案:
【答案】(1)18,12 ;(2)(4n+2),(2n+4);(3)选择第一种方式来摆餐桌.
【解析】试题分析:(1)旁边2人除外,每张桌可以坐4人,由此即可解决问题;
(2)旁边4人除外,每张桌可以坐2人,由此即可解决问题;
(3)分别求出两种情形坐的人数,即可判断.
试题解析:(1)有4张桌子,用第一种摆设方式,可以坐4×4+2=18人;用第二种摆设方式,可以坐4×2+4=12人;
(2)有n张桌子,用第一种摆设方式可以坐4n+2人;用第二种摆设方式,可以坐2n+4(用含有n的代数式表示);
(3)选择第一种方式.理由如下;
∵第一种方式,4张桌子拼在一起可坐18人.
20张桌子可拼成5张大桌子,共可坐:18×5=90(人)
第二种方式,4张桌子拼在一起可坐12人.
20张桌子可拼成5张大桌子,共可坐:12×5=60(人).
又∵90>85>60
∴应选择第一种方式来摆餐桌.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是真命题的为( )
A.四个角相等的四边形是矩形
B.四边相等的四边形是正方形
C.对角线相等的四边形是菱形
D.对角线互相垂直的四边形是平行四边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】以下各组多项式按字母a降幂排列的是( )
A.3a+a2+2
B.a2+2+3a
C.2+3a+a2
D.a2+3a+2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=
 (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的一个内角为80°,则这个等腰三角形的顶角为( )
A. 80° B. 50° C. 80°或50° D. 80°或20°
-
科目: 来源: 题型:
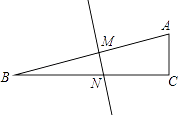
查看答案和解析>>【题目】在△ABC中,∠B=15°,∠C=90°,AB的垂直平分线交AB于点M,交BC于点N.已知BM=12cm,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题. 大家知道
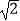 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 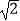 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用 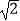 ﹣1来表示
﹣1来表示 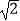 的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理的,因为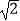 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.
请解答:已知10+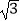 =x+y,其中x是整数,且0<y<1,求x﹣y的相反数.
=x+y,其中x是整数,且0<y<1,求x﹣y的相反数.
相关试题

