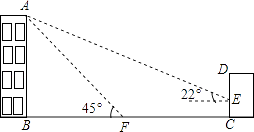
【题目】如图,某教学楼AB的后面有一建筑物CD,当光线与地面夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上),求教学楼AB的高度(sin22°≈ ![]() ,cos22°≈
,cos22°≈ ![]() ,tan22°≈
,tan22°≈ ![]() )
) 
参考答案:
【答案】解:(1)过点E作EM⊥AB,垂足为M.
设AB为x.
Rt△ABF中,∠AFB=45°,
∴BF=AB=x,
∴BC=BF+FC=x+13,
在Rt△AEM中,∠AEM=22°,AM=AB﹣BM=AB﹣CE=x﹣2,
tan22°= ![]() ,
,
则 ![]() =
= ![]() ,
,
解得:x=12.
即教学楼的高12m.

【解析】首先构造直角三角形△AEM,利用tan22°= ![]() ,求出即可;
,求出即可;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
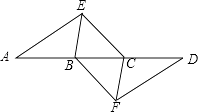
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE=时,四边形BFCE是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级有400名学生,在一次生物测验后,为了解本次测验的成绩情况,从中随机取了部分学生的成绩进行统计,并绘制了如下图表:
等级
分数
频数
频率
A
90≤x≤100
6
0.15
B
80≤x<90
20
a
C
70≤x<80
b
0.2
D
60≤x<70
c
0.15
合计
1
请你根据以上信息,解答下列问题:
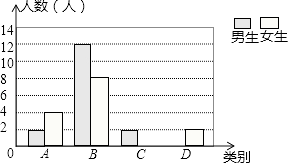
(1)a= , b= , c= , 并补全条形统计图;
(2)请你估计该校七年级共有多少名学生本次成绩不低于80分;
(3)现从样本中的A等和D等学生中各随机选取一名同学组成互助学习小组,则直接写出两名同学恰好是一名男生和一名女生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明:
如图,已知∠1、∠2互为补角,且∠3=∠B,
求证:∠AED=∠ACB.
证明:∵∠1+∠2=180°,∠2+∠4=180°
∴∠1=∠4 (______)
∴AB∥EF(_______)
∴∠3=______(______)
又∠3=∠B
∴∠B=_______(_______)
∴DE∥BC (________)
∴∠AED=∠ACB (_______)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,PD⊥AC,PE⊥AB,PF⊥BC,PD=PE=PF.求证:∠BPC=90°+
 ∠BAC.
∠BAC.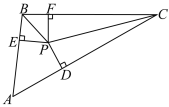
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形可以看成是线段平移得到的图形,如图1,将线段AD沿AB的方向平移AB个单位至BC处,就可以得到平行四边形ABCD,或者将线段AB沿AD的方向平移AD个单位至DC处,也可以得到平行四边形ABCD.
(1)在图2,图3,图4中,给出平行四边形ABCD的顶点A,B,D的坐标,写出图2,图3,图4中的顶点C的坐标,它们分别是_____,_______,_______;
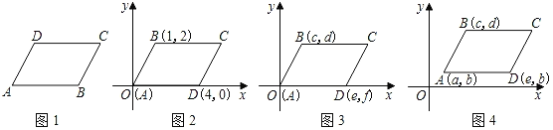
(2)通过对图2,3,4的观察和顶点C的坐标的探究,你会发现:无论平行四边形ABCD处于直角坐标系中哪个位置,当其顶点坐标为A(a,b),B(c,d),C(m,n),D(e,f)(如图5)时,则四个顶点的横坐标a,c,m,e之间的等量关系为______;纵坐标b,d,n,f之间的等量关系为_______(不必证明);
(3)如图6,在平面直角坐标系中,已知A(﹣3,0),B(3,0),C(2,4),则以A,B,C三个点为顶点的平行四边形的第四个顶点D的坐标为______.
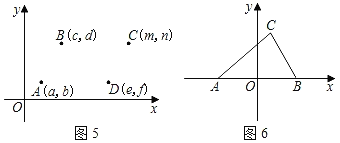
-
科目: 来源: 题型:
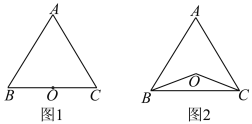
查看答案和解析>>【题目】已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在边BC上,求证:∠ABC=∠ACB;
(2)如图2,若点O在△ABC的内部,则∠ABC=∠ACB成立吗?并说明理由;
(3)若点O在△ABC的外部,则∠ABC=∠ACB成立吗?请画图表示.
相关试题

