【题目】材料一:我们可以将任意三位数记为![]() ,(其中
,(其中![]() 、
、![]() 、
、![]() 分别表示该数的百位数字,十位数字和个位数字,且
分别表示该数的百位数字,十位数字和个位数字,且![]() ),显然
),显然![]() .
.
材料二:若一个三位数的百位数字,十位数字和个位数字均不为0,则称之为初始数,比如123就是一个初始数,将初始数的三个数位上的数字交换顺序,可产生出5个新的初始数,比如由123可以产生出132,213,231,312,321这5个新初始数,这6个初始数的和成为终止数.
(1)求初始数125生成的终止数;
(2)若一个初始数![]() ,满足
,满足![]() ,且
,且![]() ,记
,记![]() ,
,![]() ,
,![]() ,若
,若![]() ,求满足条件的初始数的值.
,求满足条件的初始数的值.
参考答案:
【答案】(1)1776(2)![]() 或
或![]() .
.
【解析】
(1)根据终止数的定义即可求解;
(2)根据根据三位数的构成及x,y,z的特点表示出a,b,c的关系,再根据![]() ,且
,且![]() 即可求出a,b,c的值.
即可求出a,b,c的值.
(1)初始数125可以产生出152,215,251,512,521这5个新初始数,这6个初始数的和为1776,故初始数125生成的终止数为1776
(2)∵![]() =
=![]() =
=![]() =81
=81![]() ,
,
同理:![]() =81
=81![]() ,
,![]() =81
=81![]()
∵![]()
∴81![]() +81
+81![]() -81
-81![]() =324
=324
化简得![]()
则c(c-b)+a(b-c)=2
∴(b-c) (a-c)=2
∵a,b,c为正整数,
故![]() 或
或![]()
又![]() ,且
,且![]()
解得a=4,b=3,c=2或a=3,b=2,c=1
故满足条件的初始数的值为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】奉节脐橙是重庆市奉节县特产,中国地理标志产品,眼下,正值奉节脐橙销售旺季,某商家看准商机,第一次用4800元购进一批奉节脐橙,销售良好,于是第二次又用12000元购进一批奉节脐橙,但此时进价比第一次涨了2元,所购进的数量恰好是第一次购进数量的两倍.
(1)求第一次购进奉节脐橙的进价.
(2)实际销售中,两次售价均相同,在销售过程中,由于消费者挑选后,果品下降,第一批奉节脐橙的最后100千克八折售出,第二批奉节脐橙的最后800千克九折售出,若售完这两批奉节脐橙的获利不低于9400元,则售价至少为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 +bx+c交x轴于点A(﹣2,0)和点B,交y轴于点C(0,3),点D是x轴上一动点,连接CD,将线段CD绕点D旋转得到DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF.
+bx+c交x轴于点A(﹣2,0)和点B,交y轴于点C(0,3),点D是x轴上一动点,连接CD,将线段CD绕点D旋转得到DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF.(1)求抛物线解析式;
(2)若线段DE是CD绕点D顺时针旋转90°得到,求线段DF的长;
(3)若线段DE是CD绕点D旋转90°得到,且点E恰好在抛物线上,请求出点E的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程
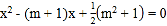 有实数根.
有实数根.(1)求m的值;
(2)先作
 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求
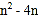 的最大值和最小值.
的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
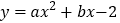 的图象与
的图象与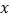 轴交于
轴交于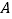 、
、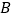 两点,与
两点,与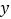 轴交于点
轴交于点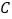 ,点
,点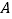 的坐标为
的坐标为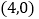 ,且当
,且当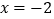 和
和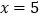 时二次函数的函数值
时二次函数的函数值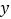 相等.
相等.(
 )求实数
)求实数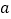 、
、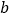 的值.
的值.(
 )如图
)如图 ,动点
,动点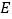 、
、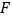 同时从
同时从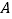 点出发,其中点
点出发,其中点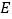 以每秒
以每秒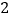 个单位长度的速度沿
个单位长度的速度沿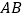 边向终点
边向终点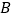 运动,点
运动,点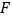 以每秒
以每秒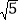 个单位长度的速度沿射线
个单位长度的速度沿射线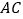 方向运动,当点
方向运动,当点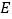 停止运动时,点
停止运动时,点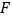 随之停止运动.设运动时间为
随之停止运动.设运动时间为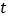 秒.连接
秒.连接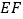 ,将
,将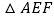 沿
沿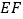 翻折,使点
翻折,使点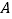 落在点
落在点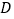 处,得到
处,得到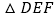 .
.①是否存在某一时刻
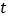 ,使得
,使得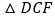 为直角三角形?若存在,求出
为直角三角形?若存在,求出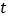 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.②设
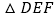 与
与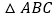 重叠部分的面积为
重叠部分的面积为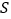 ,求
,求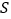 关于
关于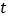 的函数关系式.
的函数关系式.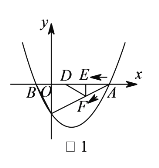
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,我们定义直线
 为抛物线
为抛物线 、b、c为常数,
、b、c为常数,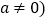 的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
已知抛物线
 与其“梦想直线”交于A、B两点
与其“梦想直线”交于A、B两点 点A在点B的左侧
点A在点B的左侧 ,与x轴负半轴交于点C.
,与x轴负半轴交于点C. 填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______;
填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______; 如图,点M为线段CB上一动点,将
如图,点M为线段CB上一动点,将 以AM所在直线为对称轴翻折,点C的对称点为N,若
以AM所在直线为对称轴翻折,点C的对称点为N,若 为该抛物线的“梦想三角形”,求点N的坐标;
为该抛物线的“梦想三角形”,求点N的坐标; 当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点
 为二次函数
为二次函数 图象的顶点,直线
图象的顶点,直线 分别交
分别交 轴正半轴,
轴正半轴, 轴于点
轴于点 ,
, .
.
(1)判断顶点
 是否在直线
是否在直线 上,并说明理由.
上,并说明理由.(2)如图1,若二次函数图象也经过点
 ,
, ,且
,且 ,根据图象,写出
,根据图象,写出 的取值范围.
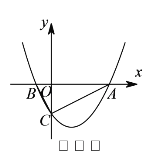
的取值范围.(3)如图2,点
 坐标为
坐标为 ,点
,点 在
在 内,若点
内,若点 ,
, 都在二次函数图象上,试比较
都在二次函数图象上,试比较 与
与 的大小.
的大小.
相关试题

