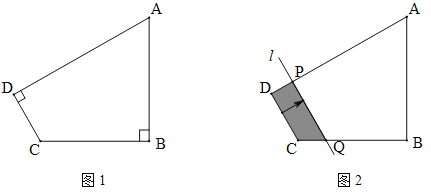
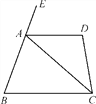
【题目】(2016四川省乐山市第23题)如图1,四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=![]() .
.
(1)求CD边的长;
(2)如图2,将直线CD边沿箭头方向平移,交DA于点P,交CB于点Q (点Q运动到点B停止),设DP=x,四边形PQCD的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出自变量
的函数关系式,并求出自变量![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() (
(![]() ).
).
【解析】
试题分析:(1)分别延长AD、BC相交于点E,在Rt△ABE中,解直角三角形可得BE,EC,AE的长,又∠E+∠A=90°,∠E+∠ECD=90°,得到∠A=∠ECD,由tanA=![]() ,得到cosA= cos∠ECD =
,得到cosA= cos∠ECD =![]() ,从而得到CD的长;
,从而得到CD的长;
(2)由(1)可知tan∠ECD=![]() ,得到ED=
,得到ED=![]() ,由PQ∥DC,可知△EDC∽△EPQ,得到PQ=
,由PQ∥DC,可知△EDC∽△EPQ,得到PQ=![]() ,由
,由![]() ,得到y=
,得到y=![]() ,而当Q点到达B点时,点P在M点处,由EC=BC,DC∥PQ,得到DM=ED=
,而当Q点到达B点时,点P在M点处,由EC=BC,DC∥PQ,得到DM=ED=![]() ,故可得自变量x的取值范围.
,故可得自变量x的取值范围.
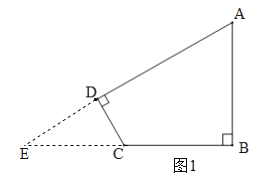
试题解析:(1)如图1,分别延长AD、BC相交于点E,在Rt△ABE中,∵tanA=![]() ,AB=3,BC=2,∴BE=4,EC=2,AE=5,又∠E+∠A=90°,∠E+∠ECD=90°,∴∠A=∠ECD,∵tanA=
,AB=3,BC=2,∴BE=4,EC=2,AE=5,又∠E+∠A=90°,∠E+∠ECD=90°,∴∠A=∠ECD,∵tanA=![]() ,∴cosA=
,∴cosA=![]() ,∴cos∠ECD=
,∴cos∠ECD=![]() ,∴CD=
,∴CD=![]() ;
;
(2)由(1)可知tan∠ECD=![]() ,∴ED=
,∴ED=![]() ,如图2,由PQ∥DC,可知△EDC∽△EPQ,∴
,如图2,由PQ∥DC,可知△EDC∽△EPQ,∴![]() ,∴
,∴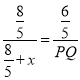 ,即PQ=
,即PQ=![]() ,∵
,∵![]() ,∴
,∴![]() ,即
,即![]() =
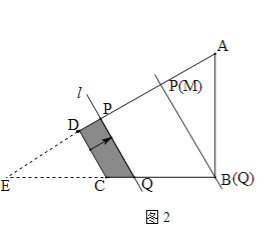
=![]() ,∴当Q点到达B点时,点P在M点处,由EC=BC,DC∥PQ,∴DM=ED=
,∴当Q点到达B点时,点P在M点处,由EC=BC,DC∥PQ,∴DM=ED=![]() ,∴自变量x的取值范围为:
,∴自变量x的取值范围为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中不成立的是( )
A.矩形的对角线相等
B.三边对应相等的两个三角形全等
C.两个相似三角形面积的比等于其相似比的平方
D.一组对边平行,另一组对边相等的四边形一定是平行四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|-7+3|=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面式子中是一元一次不等式的是( )
A.x﹣7>26
B.2x+1
C.5+4>8
D.3x=2x -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,∠D=100°,AC平分∠BCD,且∠ACB=40°,∠BAC=70°.
(1)AD与BC平行吗?试写出推理过程;
(2)求∠DAC和∠EAD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】猜谜语:“横看是圆,侧看是圆,远看是圆,近看是圆,高看是圆,低看是圆,上看、下看、左看、右看都是圆.”谜底是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果批发商场经销一种水果,如果每千克盈利5元,每天可售出200千克,经市场调查发现,在进价不变的情况下,若每千克涨价1元,销售量将减少10千克.现该商场要保证每天盈利1500元,同时又要顾客得到实惠,那么每千克应涨价元.
相关试题

