【题目】如图,在△ABC中,BC>AC , 点D在BC上,且DC=AC , ∠ACB的平分线CF交AD于F , 点E是AB的中点,连接EF . 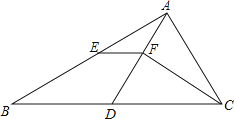
(1)求证:2EF=BD ,
(2)四边形BDFE的面积为6,求△ABD的面积.
参考答案:
【答案】
(1)解答:∵DC=AC,CF为∠ACB的平分线,
∴AF=DF,
∵AE=EB,AF=DF,
∴EF为△ABD的中位线,
∴2EF=BD.
(2)解答:∵EF为△ABD的中位线,
∴EF∥BD,2EF=BD,
∴△AEF∽△ABD
∴两三角形相似比K=1:2,
∴ =K2= ,
则4(S△ABD-6)=S△ABD,
解得:S△ABD=8.
【解析】分析:(1)根据等腰三角形性质推出F为AD中点,根据三角形的中位线定理推出即可;(2)根据三角形中位线推出EF∥BD , 推出△AEF∽△ABD且两三角形相似比K=1:2,得出面积比是 ![]() ,代入求出即可.
,代入求出即可.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△ECD均为等边三角形,B、C、D三点在一直线上,AD、BE相交于点F,DF=3,AF=4,则线段FE的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6个型号):
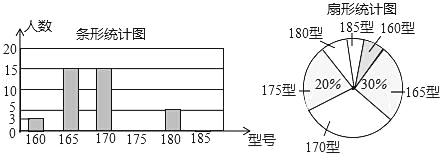
根据以上信息,解答下列问题:
(1)该班共有 名学生;
(2)补全条形统计图;
(3)该班学生所穿校服型号的众数为 ,中位数为 ;
(4)如果该校预计招收新生1500名,根据样本数据,估计新生穿170型校服的学生大约有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形ABCD中,AB∥CD , AD=BC , 点E在边AD上,BE与AC相交于点O , 且∠ABE=∠BCA .

(1)求证:△BAE∽△BOA.
(2)求证:BOBE=BCAE. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形ABCD中,AB∥DC , ∠B=90°,E为BC上一点,且AE⊥ED . 若BC=12,DC=7,BE:EC=1:2,

(1)求AB的长.
(2)求△AED的面积 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在大小为4×4的正方形网格中,是相似三角形的是( )

A.①和②
B.②和③
C.①和③
D.②和④
相关试题

