【题目】已知数轴上两点A、B对应的数分别是6,﹣8,M、N、P为数轴上三个动点,点M从A点出发,速度为每秒2个单位,点N从点B出发,速度为M点的3倍,点P从原点出发,速度为每秒1个单位.
(1)若点M向右运动,同时点N向左运动,求多长时间点M与点N相距54个单位?
(2)若点M、N、P同时都向右运动,求多长时间点P到点M,N的距离相等?
(3)当时间t满足t1<t≤t2时,M、N两点之间,N、P两点之间,M、P两点之间分别有55个、44个、11个整数点,请直接写出t1,t2的值.
参考答案:
【答案】(1)5秒;(2)![]() s或=
s或=![]() s;(3)t1=5s,t2=
s;(3)t1=5s,t2=![]() s.
s.
【解析】
(1)利用M、N之间的距离为最初的距离加上各自行驶的路程即可得到一个关于t的方程,解方程即可得出答案;
(2)先将M,N,P三点在数轴上的位置用含t的代数式表示出来,然后分点N在点P左侧和点N在点P右侧两种情况分别讨论即可;
(3)根据M,N,P之间整数点的个数,可以确定出M,N,P三点的位置,从而找到t1,t2的值
解:(1)设运动时间为t秒,
由题意可得:6+8+2t+6t=54,
∴t=5,
∴运动5秒点M与点N相距54个单位;
(2)设运动时间为t秒,
由题意可知:
M点运动到6+2t,N点运动到﹣8+6t,P点运动到t,
当t<1.6时,点N在点P左侧,
MP=NP,
∴6+t=8﹣5t,
∴t=![]() s;
s;
当t>1.6时,点N在点P右侧,
MP=NP,
∴6+t=﹣8+5t,
∴t=![]() s,
s,
∴运动![]() s或
s或![]() s时点P到点M,N的距离相等;
s时点P到点M,N的距离相等;
(3)由题意可得:M、N、P三点之间整数点的多少可看作它们之间距离的大小,
M、N两点距离最大,M、P两点距离最小,可得出M、P两点向右运动,N点向左运动
![]()
①如上图,当t1=5s时,P在5,M在16,N在﹣38,
再往前一点,MP之间的距离即包含8个整数点,NP之间有44个整数点;
②当N继续以6个单位每秒的速度向左移动,P点向右运动,
若N点移动到﹣39时,此时N、P之间仍为44个整数点,
若N点过了﹣39时,此时N、P之间为45 个整数点
故t2=![]() +5=
+5=![]() s
s
∴t1=5s,t2=![]() s.
s.
-
科目: 来源: 题型:
查看答案和解析>>【题目】经市场调查,发现进价为40元的某童装每月的销售量y(件)与售价x(元)满足一次函数关系,且相关信息如下:
售价x(元)
60
70
80
90
……
销售量y(件)
280
260
240
220
……
(1)求这个一次函数关系式;
(2)售价为多少元时,当月的利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,过C作CE⊥AD垂足为E,且∠EDC=∠BDC.
(1)求证:CE是⊙O的切线;
(2)若DE+CE=4,AB=6,求BD的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,边长为1的正方形ABCD中,AC 、DB交于点H.DE平分∠ADB,交AC于点E.联结BE并延长,交边AD于点F.
(1)求证:DC=EC;
(2)求△EAF的面积.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A地在数轴上表示的数为-16,AB两地相距50个单位长度.小明从A地出发去B地,以每分钟2个单位长度的速度行进,第一次他向左1单位长度,第二次向右2单位长度,第三次再向左3单位长度,第四次又向右4单位长度…,按此规律行进.

(1)求出B地在数轴上表示的数;
(2)若B地在原点的右侧,经过第8次行进后小明到达点P,此时点P与点B相距几个单位长度?8次运动完成后一共经过了几分钟?
(3)若经过n次(n为正整数)行进后,小明到达点Q,请你直接写出:点Q在数轴上表示的数应如何表示?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂以80元/箱的价格购进60箱原材料,准备由甲、乙两车间全部用于生产A产品.甲车间用每箱原材料可生产出A产品12千克,需耗水4吨;乙车间通过节能改造,用每箱原材料可生产出的A产品比甲车间少2千克,但耗水量是甲车间的一半.已知A产品售价为30元/千克,水价为5元/吨.设甲车间用x箱原材料生产A产品.
(1)用含x的代数式表示:乙车间用________箱原材料生产A产品;
(2)求两车间生产这批A产品的总耗水量;
(3)若两车间生产这批产品的总耗水为200吨,则该厂如何分配两车间的生产原材料?
(4)用含x的代数式表示这次生产所能获取的利润并化简.(注:利润=产品总售价-购买原材料成本-水费)
-
科目: 来源: 题型:
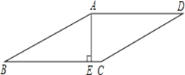
查看答案和解析>>【题目】如图,在菱形ABCD中,AE⊥BC于点E,CE=1,且AE:BC =5:13,求菱形ABCD的周长.
相关试题

