【题目】如图,⊙P的圆心为P(﹣3,2),半径为3,直线MN过点M(5,0)且平行于y轴,点N在点M的上方.
(1)在图中作出⊙P关于y轴对称的⊙P′.根据作图直接写出⊙P′与直线MN的位置关系.
(2)若点N在(1)中的⊙P′上,求PN的长.

参考答案:
【答案】(1)作图见解析,⊙P′与直线MN相交;(2)PN=![]() .
.
【解析】分析:在平面直角坐标系中,易知点P′的坐标为(3,2),⊙P′的半径和⊙P的半径相等为3,这样⊙P′就被确定,因为点N在直线MN上,直线MN过(5,0)点且平行于y轴,直线PP′⊥MN,这样利用勾股定理就可求得PN的长度.
解:(1)如图,⊙P′的圆心为(3,2),半径为3,与直线MN相交.

(2)连接PP′,交直线MN于点A,
∵点P、P′的纵坐标相同,∴PP′∥x轴,
又∵MN∥y轴,∴PP′⊥MN,
∴点A的坐标为(5,2).
在Rt△P′NA中,P′N=3,P′A=5-3=2.
∴AN=![]() =
=![]() =
=![]() ,
,
在Rt△PAN中,PA=5-(-3)=8,AN=![]() ,
,
∴PN=![]() =
=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△OAB的顶点O为坐标原点,AB∥x轴,OA=2,将等边△OAB绕原点O顺时针旋转105至△OCD的位置,则点D的坐标为( )
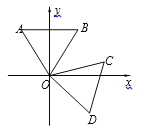
A.(2,-2)B.(
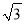 ,
,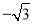 )C.(
)C.(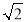 ,
,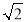 )D.(
)D.(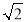 ,
,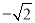 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式
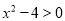 .
.解∵
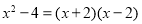 ,∴
,∴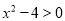 可化为
可化为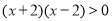 .
.由有理数的乘法法则:两数相乘,同号得正,得:①
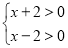 ②
②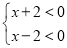
解不等式组①,得
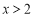 ,解不等式组②,得
,解不等式组②,得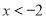
∴
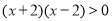 的解集为
的解集为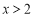 或
或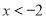 .
.即一元二次不等式
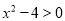 的解集为
的解集为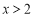 或
或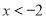 .
.(1)一元二次不等式
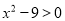 的解集为____________;
的解集为____________;(2)试解一元二次不等式
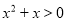 ;
;(3)试解不等式
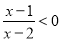 .
. -
科目: 来源: 题型:
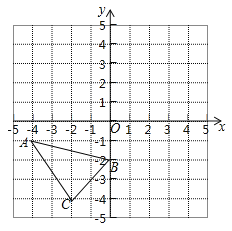
查看答案和解析>>【题目】如图,△ABC的三个顶点都在边长为1的小正方形组成的网格的格点上,以点O为原点建立直角坐标系,回答下列问题:
(1)将△ABC先向上平移5个单位,再向右平移1个单位得到△A1B1C1,画出△A1B1C1,并直接写出A1的坐标 ;
(2)将△A1B1C1绕点(0,﹣1)顺时针旋转90°得到△A2B2C2,画出A2B2C2;
(3)观察图形发现,A2B2C2是由△ABC绕点 顺时针旋转 度得到的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC,AB=AC=5,BC=6,若点P在边AC上移动,则BP的最小值是_______.
-
科目: 来源: 题型:
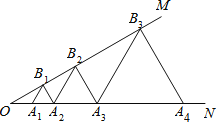
查看答案和解析>>【题目】如图,∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为______.
-
科目: 来源: 题型:
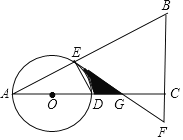
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.
(1)试判断直线EF与⊙O的位置关系,并说明理由;
(2)若OA=2,∠A=30°,求图中阴影部分的面积.
相关试题

