【题目】已知,如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求直线BC的解析式;
(3)求△MCB的面积.

参考答案:
【答案】(1)y=﹣x2+4x+5;(2)y=﹣x+5;(3)15.
【解析】
(1)由A、C、(1,8)三点在抛物线上,根据待定系数法即可求出抛物线的解析式;
(2)由B、C两点的坐标求得直线BC的解析式;
(3)过点M作MN∥y轴交BC轴于点N,则△MCB的面积=△MCN的面积+△MNB的面积=![]()
(1)∵A(﹣1,0),C(0,5),(1,8)三点在抛物线y=ax2+bx+c上,
∴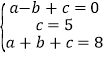 ,
,
解方程组,得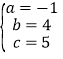 ,
,
故抛物线的解析式为y=﹣x2+4x+5;
(2)∵y=﹣x2+4x+5=﹣(x﹣5)(x+1)=﹣(x﹣2)2+9,
∴M(2,9),B(5,0),
设直线BC的解析式为:y=kx+b,
![]()
解得,![]()
则直线BC的解析式为:y=﹣x+5;
(3)过点M作MN∥y轴交BC轴于点N,
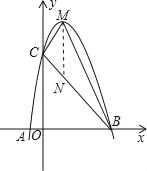
则△MCB的面积=△MCN的面积+△MNB的面积=![]()
当x=2时,y=﹣2+5=3,则N(2,3),
则MN=9﹣3=6,
则![]()
-
科目: 来源: 题型:
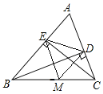
查看答案和解析>>【题目】如图,已知BD、CE是△ABC的高,M是BC边上的中点,若△EMD是等腰直角三角形,则∠A=________°
-
科目: 来源: 题型:
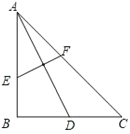
查看答案和解析>>【题目】如图,已知在△ABC中,∠B=90°,AB=BC,AD是BC边上的中线,EF是AD的垂直平分线,交AB于点E,交AC于点F,则AE:BE的值为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位,再向左平移1个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)作出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2,并直接写出C2点的坐标;
(3)求△A2B2C2面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】冬至过后,昼夜温差逐渐加大,山城的市民们已然感受到了深冬的寒意.在还未普遍使用地暖供暖设备的山城,小型电取暖器仍然深受市民的青睐.某格力专卖店销售壁挂式电暖器和卤素/石英式取暖器(俗称 “小太阳”),其中壁挂式电暖器的售价是“小太阳”售价的5倍还多100元,2016年12月份壁挂式电暖器和“小太阳”共销售500台,壁挂式电暖器与“小太阳”销量之比是4∶1,销售总收入为58.6万元.
(1)分别求出每台壁挂式电暖器和“小太阳”的售价;
(2)随着“元旦、春节”双节的来临和气温的回升,销售进入淡季,2017年1月份,壁挂式电暖器的售价比2016年12月下调了4m﹪,根据经验销售量将比2016年12月下滑6m﹪,而“小太阳”的销售量和售价都维持不变,预计销售总收入将下降到16.04万元,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角△ABC中,∠ACB=90°,CA=CB,CD为斜边AB上的中线.
(1)如图1,AE平分∠CAB交BC于E,交CD于F,若DF=2,求AC的长;
(2)将图1中的△ADC绕点D顺时针旋转一定角度得到△ADN,如图2,P,Q分别为线段AN,BC的中点,连接AC,BN,PQ,求证:BN=
 PQ.
PQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个n位自然数
 能被x0整除,依次轮换个位数字得到的新数
能被x0整除,依次轮换个位数字得到的新数 能被x0+1整除,再依次轮换个位数字得到的新数
能被x0+1整除,再依次轮换个位数字得到的新数 能被x0+2整除,按此规律轮换后,
能被x0+2整除,按此规律轮换后, 能被x0+3整除,…,
能被x0+3整除,…, 能被x0+n﹣1整除,则称这个n位数
能被x0+n﹣1整除,则称这个n位数 是x0的一个“轮换数”.
是x0的一个“轮换数”.例如:60能被5整除,06能被6整除,则称两位数60是5的一个“轮换数”;
再如:324能被2整除,243能被3整除,432能被4整除,则称三位数324是2个一个“轮换数”.
(1)若一个两位自然数的个位数字是十位数字的2倍,求证这个两位自然数一定是“轮换数”.
(2)若三位自然数
 是3的一个“轮换数”,其中a=2,求这个三位自然数
是3的一个“轮换数”,其中a=2,求这个三位自然数 .
.
相关试题

