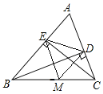
【题目】如图,已知BD、CE是△ABC的高,M是BC边上的中点,若△EMD是等腰直角三角形,则∠A=________°
参考答案:
【答案】45
【解析】
首先根据直角三角形斜边上的中线等于斜边的一半,得出BM=EM=CM=DM,进而得出∠ABC=∠BEM,∠ACB=∠CDM,又根据△EMD是等腰直角三角形,得出∠EMD=90°,通过等量转换,即可得出∠A.
∵BD、CE是△ABC的高,M是BC边上的中点,
∴BM=EM=CM=DM,
∴∠ABC=∠BEM,∠ACB=∠CDM,
又∵△EMD是等腰直角三角形,
∴∠EMD=90°
∴∠BME+∠CMD=90°=(180°-2∠ABC)+(180°-2∠ACB)=360°-2(180°-∠A)
∴∠A=45°
-
科目: 来源: 题型:
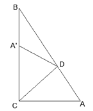
查看答案和解析>>【题目】如图Rt△ABC中∠ACB=90°,将其折叠使点A落在边BC的点A′处,折痕为CD,若∠A′DB=20°,则∠B=( )
A.45°B.35°C.30°D.40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】AD与BE是△ABC的角平分线,D,E分别在BC,AC上,若AD=AB,BE=BC,则∠C=( )

A. 69° B.
 C.
C.  D. 不能确定
D. 不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲乙两艘巡逻艇立即从相距13海里的A、B两基地前去拦截,6分钟后同时到达C地成功将其拦截,已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,航向为北偏西40°,则甲巡逻艇航向为北偏东________°
-
科目: 来源: 题型:
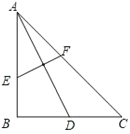
查看答案和解析>>【题目】如图,已知在△ABC中,∠B=90°,AB=BC,AD是BC边上的中线,EF是AD的垂直平分线,交AB于点E,交AC于点F,则AE:BE的值为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位,再向左平移1个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)作出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2,并直接写出C2点的坐标;
(3)求△A2B2C2面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求直线BC的解析式;
(3)求△MCB的面积.

相关试题

